Using Coq to Verify SPARK 2014 Code
by Yannick Moy –
In the first release of SPARK 2014, GNATprove only provided support for automatic provers, in particular Alt-Ergo.
Automatic provers are very handy when it comes to perform a big numberof simple proof. But they can fail to prove valid formulas when the proof involves some advanced reasoning. As mentioned in a previous post, one check left unproved might invalidate assumptions on which are based the proofs of multiple other checks. This is a case where manual proof may be useful for SPARK 2014 users.
The development version of GNATprove now supports Coq to perform manual proof. Coq is an interactive proof assistant. Coq allows users to perform mathematical proof guaranteed to be rigorous and free from human mistakes.
To prove a formula with Coq, the user writes a "proof scripts". A proof script is composed of different Coq instructions named tactics. Each tactic represents the operation being the transition between one state of the proof and the next one. A Coq proof starts with one subgoal, i.e. the formula we want to prove. Each tactic applies to one subgoal an can produce an arbitrary number of subgoals (including 0). The initial formula is proved once there are no subgoals remaining.
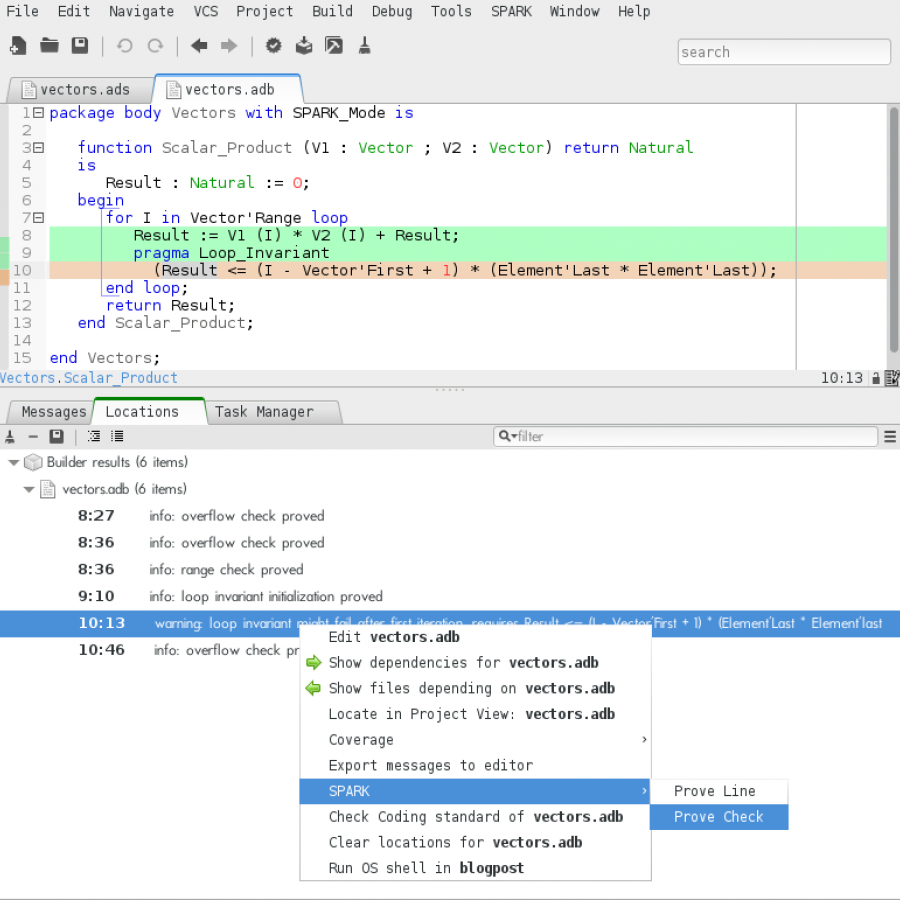
Let's see how to use Coq on some simple SPARK 2014 code from the GPS environment:
package Vectors with SPARK_Mode is
subtype Element is Positive range 1 .. 100;
subtype Index is Positive range 1 .. 100;
type Vector is array (Positive range 1 .. 100) of Element;
function Scalar_Product (V1 : Vector; V2 : Vector) return Natural;
end Vectors;
package body Vectors with SPARK_Mode is
function Scalar_Product (V1 : Vector ; V2 : Vector) return Natural
is
Result : Natural := 0;
begin
for I in Vector'Range loop
Result := V1 (I) * V2 (I) + Result;
pragma Loop_Invariant
(Result <= (I - Vector'First + 1) * (Element'Last * Element'Last));
end loop;
return Result;
end Scalar_Product;
end Vectors;First, we analyse the code with the SPARK/Prove All menu to get the results of flow and automated proof:
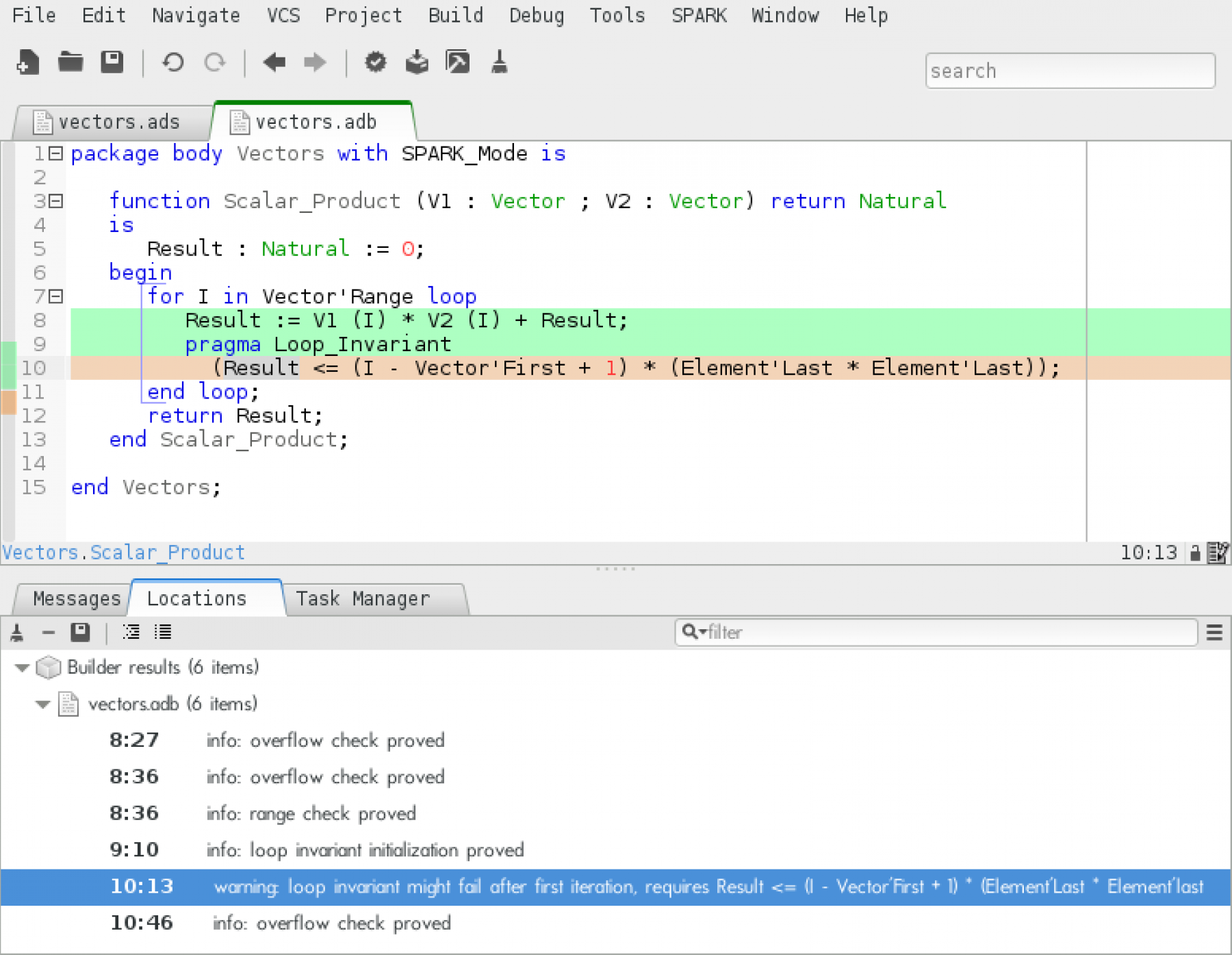
Here, the loop invariant is needed to prove that there will be no overflow errors, but Alt-Ergo is not capable of proving the preservation of the invariant. To prove it with Coq we first select the failing check and choose the menu SPARK/Prove Check and indicate Coq as alternate prover:
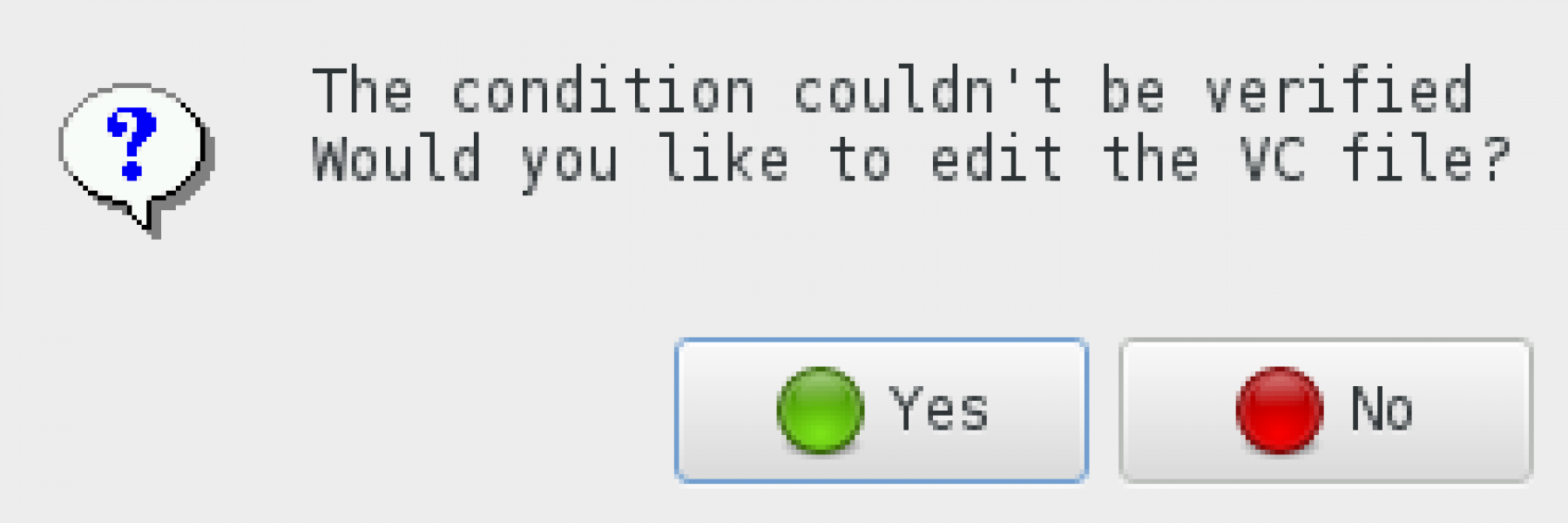
If it is the first time we try to prove this check with Coq, GNATprove will generate a new file containing the corresponding VC in Coq syntax. If the analysis fails (i.e. there was no proof with Coq for this check or the proof is invalid), GPS will suggest to edit the Coq file:
Editing the file will open a new editor adapted for the chosen interactive prover (this will require some preliminary configuration for Why3). The file presented to us contains many axioms corresponding to the formal definitions of SPARK 2014 types and subprograms. These will be needed to have some properties about the values manipulated during the proof. At the end of the file, we find the VC formula we have to prove to be certain of our loop invariant preservation:
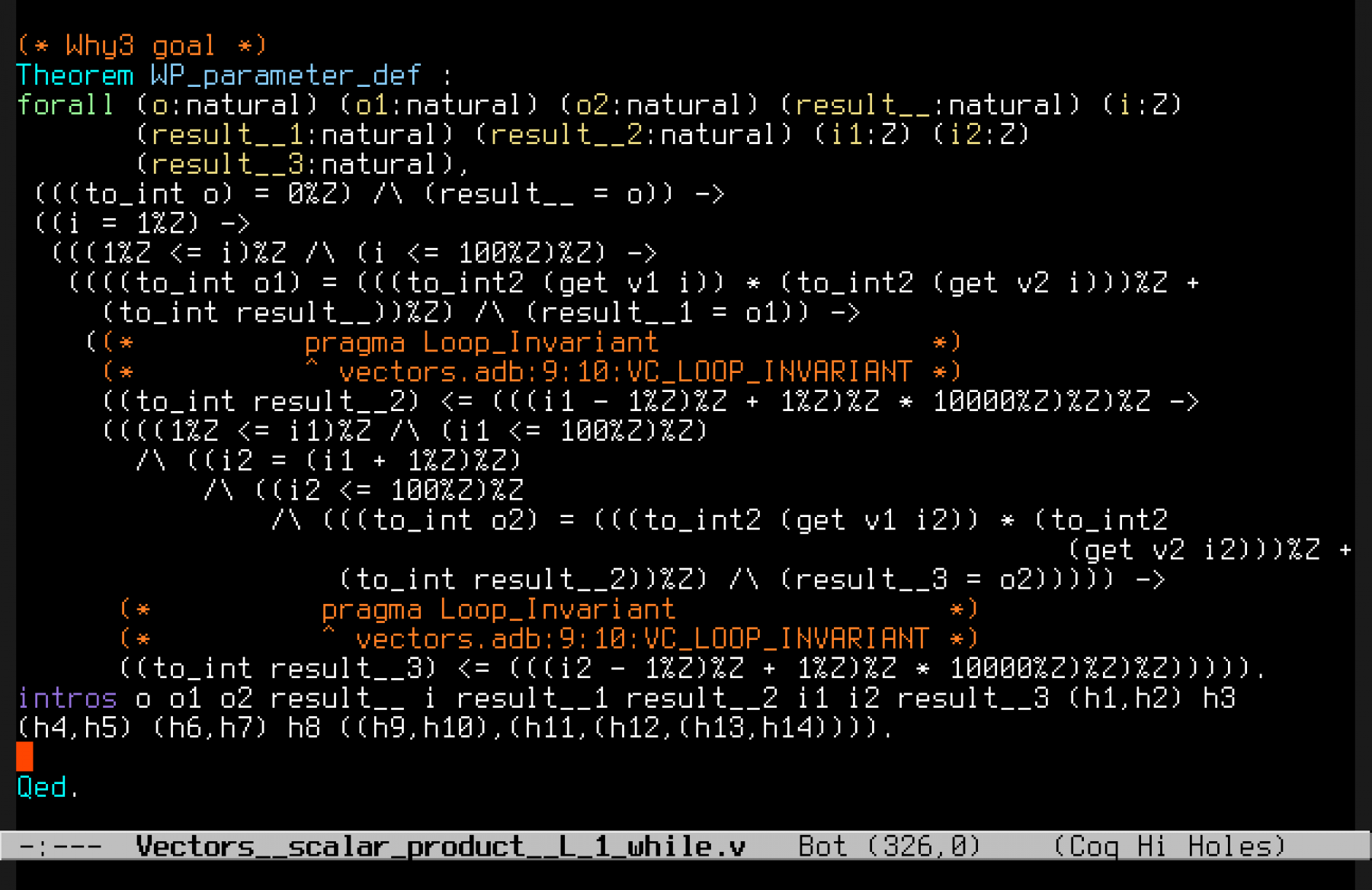
The proof is to be completed between the introductions of variable and hypothesis in the proof context and the "Qed." proof terminator.
The reason for launching a new editor from GPS instead of writing the proof in GPS is that editors for manual proof offer an interactive display of the state of the proof (i.e. what is in the context? how many subgoals are there and what are these subgoals). This is really essential when writing a proof since proof scripts can become easily confusing when they are long or when one doesn't know exactly how each tactic he uses in the proof works.
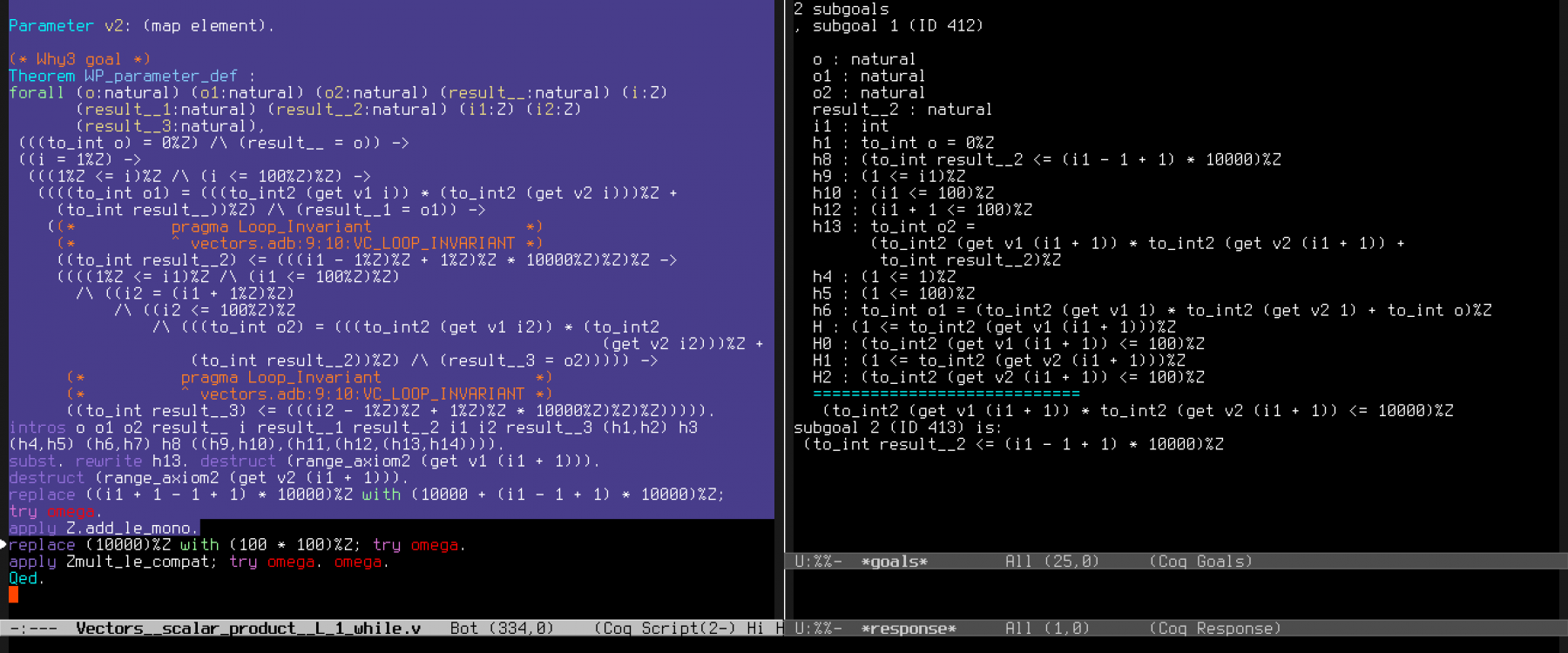
The editor buffer on the right displays the state of the proof, on the left we can see highlighted in blue what has been already processed by Coq. In this state, we have two subgoals to the proof. Only one subgoal is "focused" at a given moment.
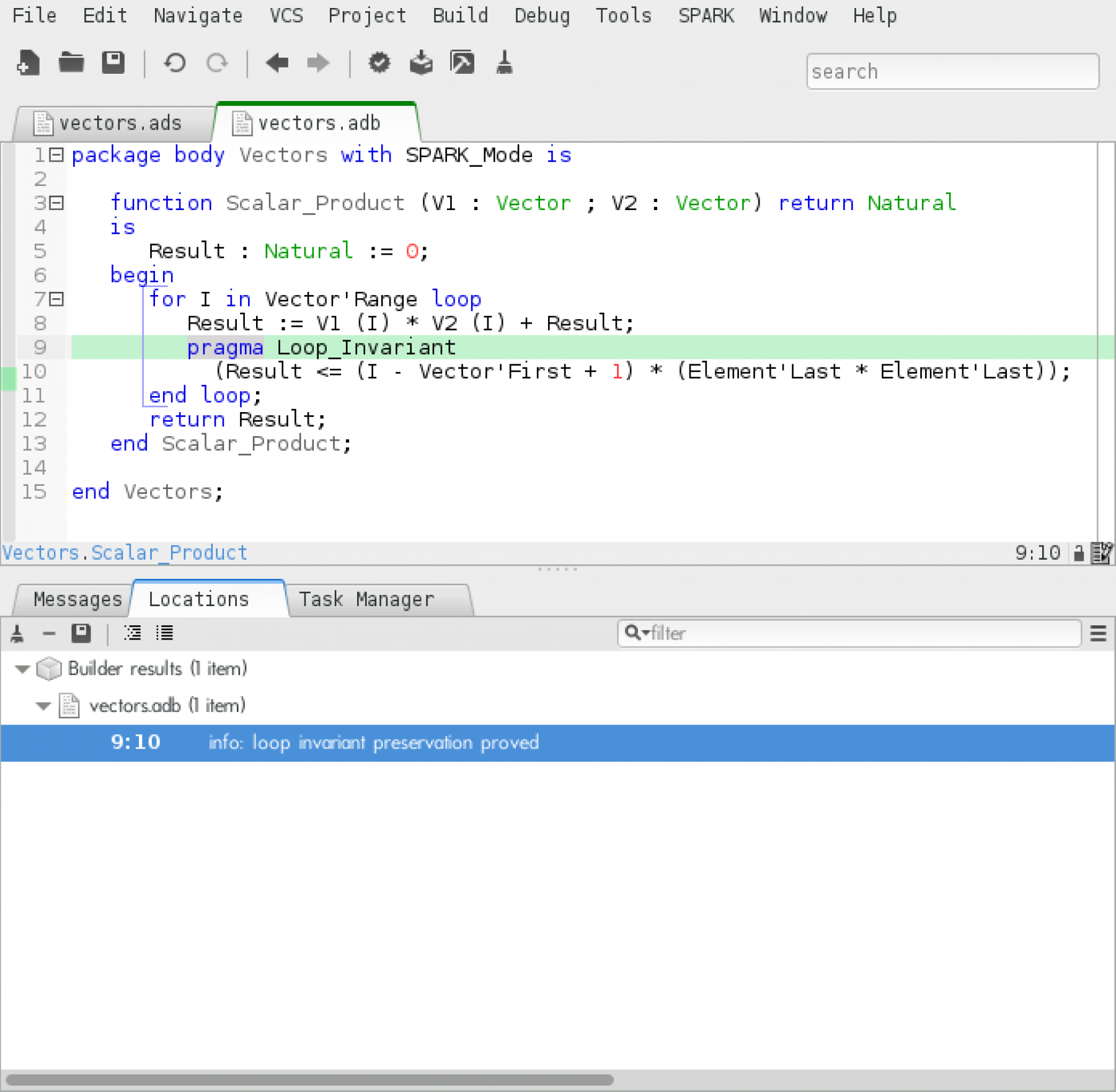
Once the proof is finished, we can close the editor and GPS will offer to re-run the "Prove Check" operation in order to validate our proof. Now our loop invariant preservation is proved:
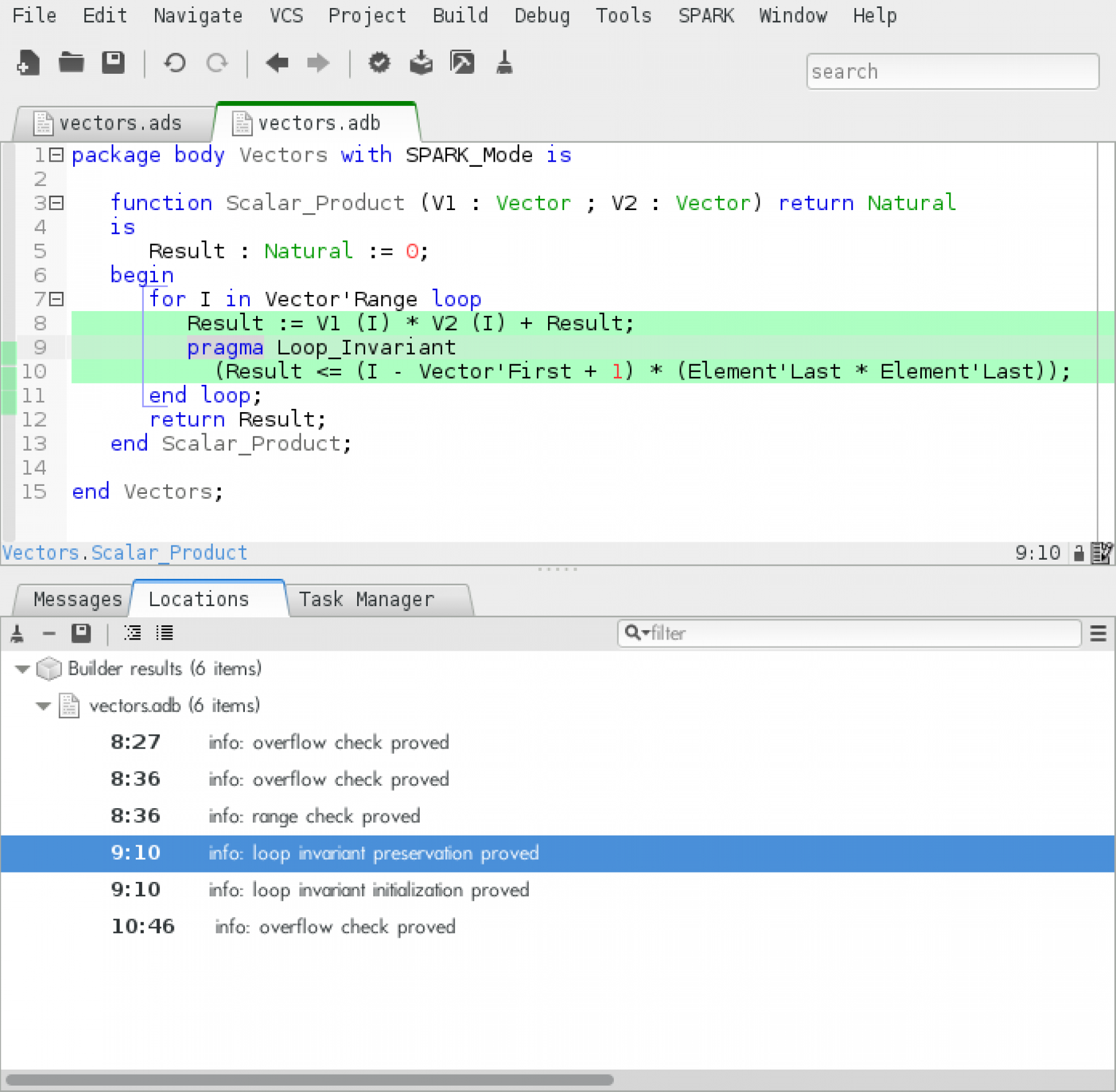
Now we can re-run "Prove All" and see that our function is now fully verified by GNATprove:
To know more about this new capability of GNATprove, see the following sections of the SPARK User's Guide:
About Yannick Moy
Yannick Moy is Head of the Static Analysis Unit at AdaCore. Yannick contributes to the development of SPARK, a software source code analyzer aiming at verifying safety/security properties of programs. He frequently talks about SPARK in articles, conferences, classes and blogs (in particular blog.adacore.com). Yannick previously worked on source code analyzers for PolySpace (now The MathWorks) and at Université Paris-Sud.