As a programming language, Ada offers a number of features that require runtime support, e.g. exception propagation or concurrency (tasks, protected objects). The GNAT compiler implements this support in its runtime library, which comes in a number of different flavors, with more or less capability. The GNAT light runtime library is a version of the runtime library targeted at embedded platforms and certification, with an Operating System or without it (baremetal). It contains around 180 units focused mostly on I/O, numerics, text manipulation, memory operations.

Variants of the GNAT light runtime library have been certified for use at the highest levels of criticality in several industrial domains: avionics (DO-178), space (ECSS-E-ST40C), railway (EN 50128), automotive (ISO-26262). Details vary across certification regimes, but the common approach to certification used today is based on written requirements traced to corresponding tests, supported by test coverage analysis. Despite this strict certification process, some bugs were found in the past in the code. An ongoing project at AdaCore is applying formal proof with SPARK to the light runtime units, in order to prove their correctness: that the code is free of runtime errors, and that it satisfies its functional specifications. So far, 40 units (out of 180) have been proved, and a few bugs fixed along the way (including a buffer overflow).

But first, let’s consider a motivating example of why one may need formal proof to get confidence in the correctness of runtime units. Back in 2012, the late great programmer (and co-founder of AdaCore) Robert Dewar implemented runtime support for big integers in the GNAT compiler, in order to allow intermediate arithmetic computations without overflows (say, if you compute (A * B) / C but (A * B) might overflow, this allows you to tell the compiler to compute (A * B) / C with big integers, so that only the final result has to fit in a machine integer). The most complex function was the division between big integers, for which he implemented algorithm D by Donald Knuth from The Art of Computer Programming Vol 2, 2nd Edition - 1981, section 4.3.1. One of the code reviewers reported a possible integer overflow in a test, when computing the quantity ((u (j) & u (j + 1)) - DD (qhat) * DD (v1)) * b. Robert was initially not worried, given that this closely followed Knuth’s published algorithm, but got concerned when it was shown that the overflow could be exercised! So that the computation of (A * B) / C with A = 18446744069414584318, B = 4294967296 and C = 18446744069414584319 was giving the result 2147483648 instead of the correct 4294967295.

Thankfully, we were not the first to spot the bug, which had already been corrected in 1995. Here is the relevant section of errata of TAOCP Vol 2, 2nd Edition, replacing the buggy test with new code (to the right of the strange arrow):

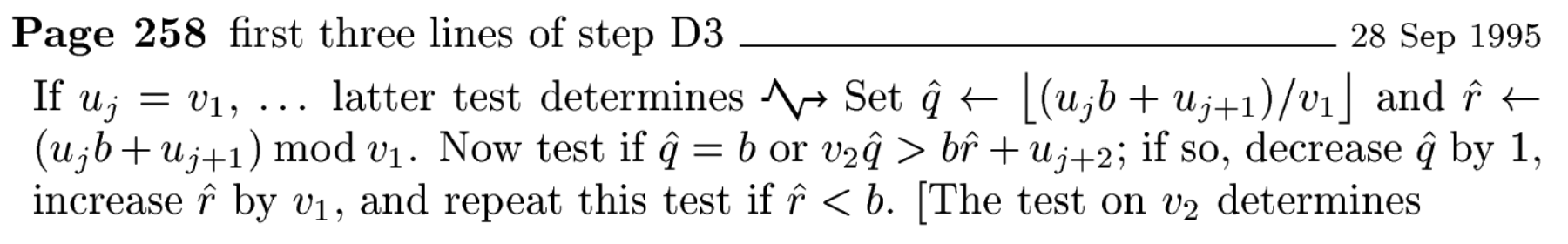
In fact, with this patch, the rewritten test might still lead to an overflow! This was detected a decade later, in 2005. Here is the relevant section of errata of TAOCP Vol 2, 3rd Edition, changing the comparison operation:

After careful code reviews, we convinced ourselves that the new version was correct, but, already at the time, we wondered whether this could be proved using SPARK tools (after all, the GNAT compiler is written itself in Ada, so we could hope to prove part of it). That was not possible at the time, but we kept it as a future challenge.

Of course, the same algorithm may get implemented numerous times in a given application, and GNAT was no exception. There were two other implementations of algorithm D in GNAT, one in uintp.adb for arbitrary-precision computation at compile time, and one in s-arit64.adb for runtime support of fixed-point arithmetic. In the specific context of these two other implementations, we found no clear bug: the fixes were propagated to uintp.adb which was using a similar test, while s-arit64.adb used a different comparison which could not overflow. But given that the 1st Edition of Vol 2 was published in 1969, there must be hundreds of implementations of this algorithm out there that did not apply later fixes and are still incorrect!

Five years later, in 2019, our interest in the implementation of algorithm D in s-arit64.adb was raised by a remark of an external auditor, as part of the certification of this runtime unit for use in space. The auditor noted the high complexity of this function and asked for the addition of more comments in the code to be able to assess its correctness. Prompted by this request, we reviewed again this implementation and discovered that the code failed to raise an exception in a case where it should have done so (because the result of the division was too large), and that the code of another function in that unit contained two possible integer overflows when converting between signed and unsigned values. Thankfully, none was critical, because the former concerned a case of incorrect inputs, and because the overflows in the latter were silent in the runtime at that time (the runtime was compiled without runtime checking). Still, that was a close-enough call for us to wish that we could increase our confidence in the correctness of this code through proof.

And this is what we did in the summer of 2021! Our intern Pierre-Alexandre Bazin used SPARK to prove that s-arit64.adb was correctly implementing all its functions: there were no possible runtime errors in the code, and all the functions implemented their specification faithfully. This required expressing the specification as contracts in SPARK, that is, preconditions and postconditions, like here for the function Scaled_Divide implementing algorithm D:

The postcondition uses big numbers to express that the resulting quotient Q is the mathematical operation (X * Y / Z) and the resulting remainder R is the rounded value of the mathematical remainder. The precondition states that these values for Q and R should fit in the machine integer type Double_Int. See the code for the definition of the ghost functions Round_Quotient and Same_Sign which are used to define this contract.

The implementation of Scaled_Divide was slightly modified to make it provable, but more critically, Pierre-Alexandre had to use quite a lot of ghost code to guide automatic provers, including basic arithmetic lemmas to enunciate and prove mathematical properties, as well as a number of more complex lemmas to isolate parts of the proof, and a few intermediate assertions to simplify and share the proofs between provers.

Encouraged by this initial success, we have added contracts expressing the full functional specification of many other units in the GNAT light runtime, and proved with SPARK that the code correctly implemented these contracts. This includes units for character and string handling (like a-strsup.ads/a-strsup.adb), units for support of language attributes ‘Width, ‘Value and ‘Image (like s-widthu.ads/s-widthu.adb, s-valueu.ads/s-valueu.adb and s-imageu.ads/s-imageu.adb), support for exponentiation (like s-exponn.ads/s-exponn.adb). We have so far proven 40 such units, and, along the way, we have discovered and fixed a few cases of overflow check and range check failures, one of which could lead to a buffer overflow on a runtime built without runtime checks. As you can see from the source files, that required adding many specifications (around 400 preconditions and 500 postconditions) and ghost code (around 150 loop invariants, 400 assertions, 300 ghost entities), and the daily proof takes 1.5 hours on a Linux server with 36 cores.

Most remaining units remain out of reach for SPARK today, either because they rely on an untyped memory model (converting between raw Address values and typed pointers) or because they require precise reasoning on bitwise floating-point representation. Most units that use Address-to-pointer conversions use very simple algorithms, and those that manipulate floating-point values are direct translations in Ada of either reference C implementations or textbook algorithms, which increases confidence in their correctness. Our vision for the future is to both maintain the automatic proof of the 40 units proved so far as the analysis tool and provers get updated, so that we can benefit from the associated assurance in certification, and to grow the set of proved units as SPARK language allows more constructs and tooling improves.

The fact that this effort has not led to the discovery of serious bugs is a testament to the quality of the GNAT light runtime code, which has been submitted to a very high level of scrutiny in the past 20 years as it has been certified to the highest levels of multiple certification standards for avionics, railway, space, etc. Proof with SPARK is a new way to achieve this high level of assurance, with stronger guarantees about the absence of whole classes of errors, and about the faithfulness of all code paths to the specification.

This work was presented in the Ada devroom at FOSDEM 2022.