Sorting algorithms are to computer science what “Hello World!” is to programming. A way for beginners to get their hands dirty. Which also means that most programmers don’t write “Hello World!” programs past their studies, and computer scientists don’t look at sorting algorithms past their PhD.

Which made it surprising that a new “interesting” sorting algorithm was published at the end of 2021, whose appeal drew attention from both computer scientists and programmers. Here is the algorithm in full details:

As an expert user of Ada, and an anecdotal user of SPARK, one of us (Lionel) took it as a challenge to try some functional proof with SPARK. Despite a hopeful start, this ended up badly. As a SPARK expert thus contacted to help with the challenge, one of us (Yannick) took it as a way to show how functional proof should be approached in SPARK. Including some false starts, this ended up well (and under an hour). This is the story of this challenge, and the tips we think are important to share with those who aim at functional proof with SPARK.

I am Lionel, I’ll start.

I recently stumbled upon a tweet about a paper on an “unbelievable” sorting algorithm:

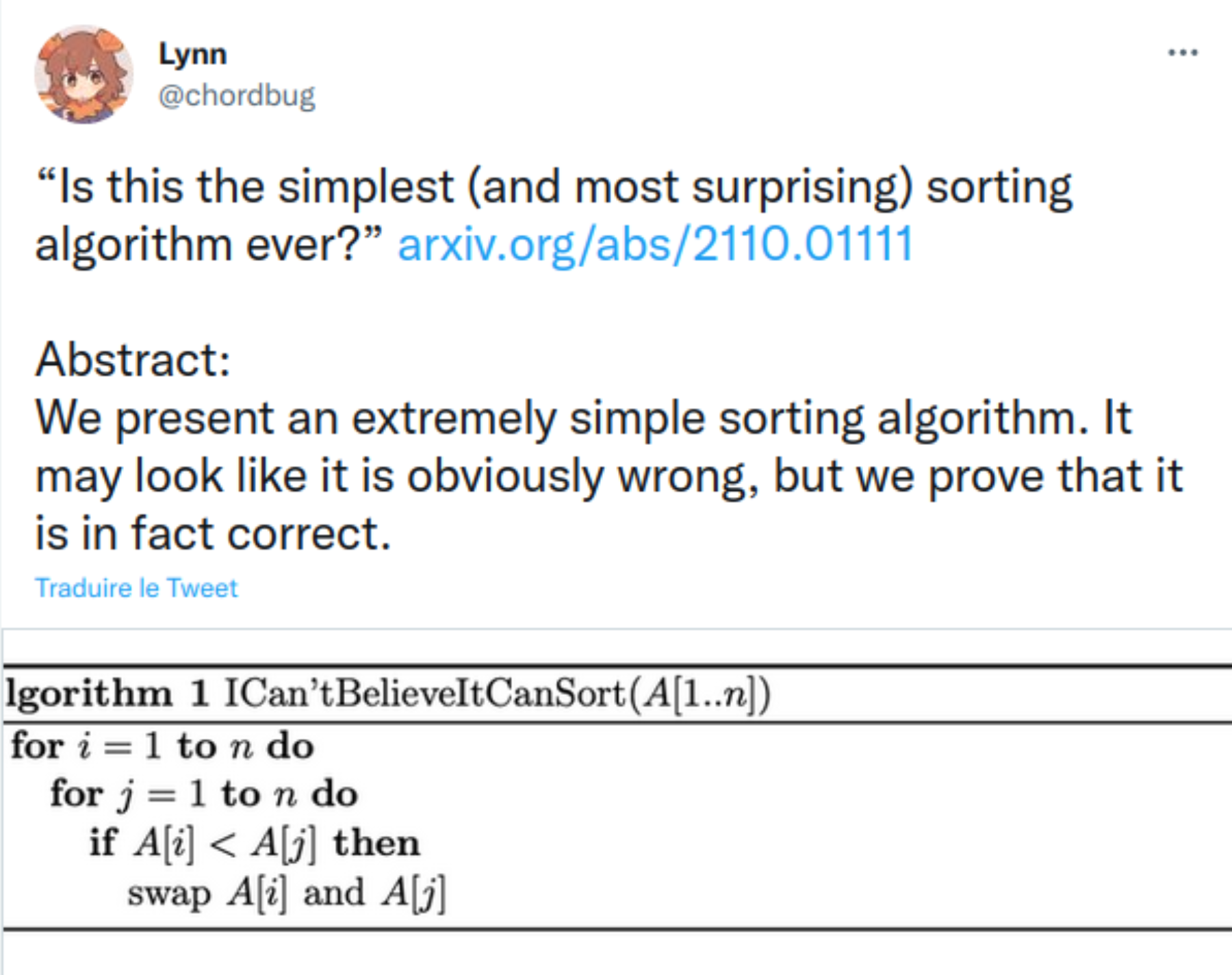
I read the paper intro, and couldn’t realize what was wrong with it instinctively, but quickly seeing all the replies to the tweet brought back memories of learning programming, writing cool (at the time) programs for years, and then later on getting some formal computer science education.

I dug up my first ever sorting algorithm. I’d used it in a silly 3D renderer that I’d implemented in 2000 on a Pentium 75, all implemented from scratch from what some might call nowadays “first principles” (i.e. I had absolutely no clue what I was doing). In a 3D renderer, once you’ve got your list of triangles to paint, and the direction of the camera set up, you want to z-sort the triangles so you can run the Painter algorithm (Wikipedia here is very generous, and calls it “depth-sort algorithm”). I needed a sort algorithm and I had no books, just my C compiler, SDL headers and some old French magazines about setting up VESA…

So I built one. I mean I built this one, and to me it looked like it worked. If you look at this video, it makes sense, somehow, especially for small array sizes, for a beginner that has no notion of smart sorting, big-O notation and no internet. My “unit tests” (generous term again) from the time show how little I understood about testing because they seem to be chosen for this algorithm (to validate this implementation and not sorting in general).

I’d put it together without videos and all the fancy visualizations one can use when learning sorting algorithms, and I didn’t think about this code for years afterwards.

When I later learned Ada, first year of formal studies, I needed a sort function for a project and I just ported that algorithm and went with it (and I lived with it until I some month later I had to sort 2 millions entries and after a night at 100% CPU with almost no progress, I caved and cracked my copy of Sedgewick and started learning the science and not just the hacking-stuff-up).

Paraphrasing the old code, it looked very simple:

Tip: Start small (simple small data types, a single subprogram)

When I read the tweet and all the replies, I admit I felt compassion for old me (well, young me), even though I saw other people admitting they’d come up with this sorting algorithm once upon a time. I wondered whether applying modern tech (other than having a sorting algorithm in the standard library and knowing about it…) blindly would comfort such a developer in his or her “wrong” version. I decided to launch myself a challenge: proving the algorithm using SPARK, without looking at the proof in the paper. Should be easy enough, right (famous last words)?

I fired up the ultimate Ada IDE (vim) and just copy-pasted the old code, compiled it (gnatmake -gnatA stupid_sort.adb) and ran it (through gdb to get the content of A after Sort returns). It works, for that input.

Tip: Start with a passing test

Then I wanted to prove that Sort sorts all possible arrays so I added the SPARK pixie dust:

and the necessary post-condition for Sort:

Which reads:

• when the Sort procedure returns

• for every element A(J) of the array (except the last one)

  • the element A(J) is smaller or equal to the next element A(J+1)

Then I created a GPR project to run GNATprove:

And on I went:

Which was kind of expected, but there’s a --level knob, if you’re lazy like me you’ll just try it whenever you find something GNATprove balks at (sadly it only goes to 4, you can’t turn it to eleven… yet):

And… GNATprove managed to prove the functional correctness of that postcondition!

Tip: Use proof automation (and turn up the knob)

Let’s check the synthesis of what GNATprove did (the gnatprove.out file):

Here GNATprove tells us it managed to prove our postcondition (a functional contract) with Z3. So it works! SPARK can prove the algorithm! Victory? Not so fast.

Let’s try to go for larger array sizes, e.g. 1 .. 10. Now after 16 seconds, GNATprove goes back to:

Turning the level up to the max (--level=4) doesn’t get us better results, but takes more than 3 minutes, for the same result. So back to square one.

The first reflex I had (wrongly) ingrained was to try and state obvious things through assertions. Keep in mind I didn’t want to read the paper, with the many juicy proofs and insights it might contain. So there I went:

First I put the swap code in its own procedure:

… which (spoiler) wasn’t a very good idea (see “framing conditions”, later). I didn’t get better results, so I went on adding assertions.

At some point I ended up with lots of tautological asserts, and it felt more and more like I really didn’t understand what the problem was.

And still, no progress on the proof of the postcondition.

Tip: Avoid the Assertocalypse

The message from GNATprove was hinting at a Loop_Invariant:

So I looked at the videos of the sort again, and came up with two (very wrong) loop invariants:

This made GNATprove very mad:

Tip: Understand tool messages

That’s when I decided to call up my local SPARK friend Yannick, to teach me about loop invariants, and how you prove such an algorithm with SPARK.

Tip: Have an expert on call

I am Yannick, I’ll jump in.

Let’s return first to the addition of the Swap procedure in Lionel’s code. Remember the postcondition he wrote for Swap:

That’s true, but not sufficient. Indeed, all the provers know about variable A after a call to Swap (since this parameter is modified in Swap) is what the postcondition of Swap says about it. And… it says nothing about all the values of A outside of indexes I and J! So there is no chance that GNATprove will be able to prove our sorting code.

This need to identify what has changed during a call with enough precision is known as the frame condition, and it’s a typical beginner’s mistake to forget it. Here, a suitable postcondition would be:

which states exactly the content of A after a call to Swap.

Tip: Beware the frame condition

Ironically, you get the same result if you don’t specify a postcondition at all on Swap, because GNATprove will inline the call in that case! Inlining of calls and unrolling of loops are powerful techniques for automating the proof of programs, without the need for a user to specify contracts and loop invariants. But as usual with automation, the risk is that, when the situation gets more complex, automation fails and the user is left with a complex situation that she does not understand (a.k.a. the curse of automation). Loop unrolling explains why Lionel was initially "feeling lucky!" with Z3 proving the postcondition of Sort for small array sizes, without having to write loop invariants. But the curse of automation stroke back when increasing the array size, as the loops are not unrolled anymore, or the unrolling leads to unmanageable formulas for automatic provers.

One way to remain aware of the choices in terms of automation made by GNATprove is to use the switch --info which outputs such information:

Tip: Use the right tool configuration (and switches!)

Contrary to the heroic (masochistic?) Lionel, I did not aim at rediscovering how the algorithm worked by looking at the code. Instead, I took the time to read the short article, and to convince myself that I understood why it worked.

Tip: Understand the code that you want to prove

Well, at least I thought I understood the algorithm. More on that later.

I started by defining suitable types for the index of the array, one being slightly larger than the other, in order to accommodate empty ranges of values (when we start the iteration):

Tip: Define suitable types with the tightest constraints

Types are the best specifications, because you get their properties everywhere a value of the type is used, without having to repeat the properties in assertions, preconditions, etc.

Then, I defined expression functions for the important properties used in the article: that the array over a given range is sorted, and that the maximum of the array over a given range is at a given index.

Tip: Define suitable expression functions for important properties

In general, it’s better to give a name to important properties that will be used multiple times in specifications, assertions and ghost code, because it makes the specification and proof more readable, and because it can help automatic provers. Here, it’s all the more helpful for automatic provers because it isolates quantifiers “for all”.

The form of these properties is also quite important. Instead of using the natural expression of sortedness as “every element is less or equal to the next”, I have expressed it as the equivalent transitive closure of this property, that is, “every element is less or equal to every element that follows”. That makes a big difference for automatic provers, as establishing the latter from the former requires inductive reasoning, which automatic provers are poor at, while the former is immediately deduced from the latter.

Similarly, I could have defined Is_Max as a function that takes as input the maximum Max of the array over a given range, instead of the index M of the maximum, and computes the conjunction:

But this uses an existential quantification “for some” which is hard to establish for automatic provers, as this requires exhibiting the “witness” index M here. So I went for the definition that did not require an existential quantification, by passing the index M as parameter instead.

Tip: Use idiomatic definitions of properties that help automatic provers

With these definitions, the loop invariant of the external loop can be expressed very easily, based on the properties of that loop described in the article:

It gets a bit trickier for the internal loop, as the explanations in the article in terms of values of K before and after I cannot be directly translated into loop invariants. Plus the article talks of going from index I to index I+1 while the code goes from index I-1 and index I (when expressing the loop invariant). That’s where I tried out various loop invariants in my head, with the support of pen-and-paper to understand how the algorithm really worked. And it went 💡 the array stayed sorted at every iteration of the internal loop for all indexes lower than I!

And during the internal loop, the maximum value over the whole array was either located at index I-1 (at the beginning of the iteration) or at index I (after getting to iteration J = I-1):

Tip: Use pen-and-paper to really understand the code that you want to prove

It’s all too easy to “understand” that something works by going through the steps of an explanation/demonstration (like in the article), without being able to really understand why it works. Proof requires us to understand why it works.

As GNATprove could not prove the loop invariant of the inner loop, even at level 4 (all provers get called at that level, with a substantial timeout of 60 seconds per check), I tried running the program through its test with assertions enabled, and… the loop invariant failed at runtime! No wonder GNATprove could not prove it.

Tip: Execute assertions during tests to help debug them

Just looking at the failing loop invariant, I realized that it could not be true during the first iteration of the loop, where we have not yet identified the maximum value of the array. So I added a special case for I=A’First:

But the test was still failing at runtime! This time, I ran the test in the debugger (gdb inside GNAT Studio), to display values of all variables when hitting the failing loop invariant. That was a case of off-by-one error, the test “J < I” in the definition of constant M should be “J < I-1”. With that, the test was running without error.

Tip: Debug failing assertions by running tests with assertions in the debugger

I reran GNATprove on the code. It reported cases of runtime errors when calling functions Sorted/Is_Max, which I fixed. But GNATprove could still not prove the loop invariant of the internal loop stating that A remained sorted from A’First to I-1. I read again the explanations in the article, which confirmed that it was true. Yet it was not proved. So I looked at the code, to see how the loop invariant at iteration J can be deduced from the loop invariant at iteration J-1 and the execution of the current iteration. And it was not provable! Because we were missing the information that, up to value J=I-1, the value at index I is greater than all values seen so far:

Now, GNATprove proves the code easily (at level 2).

Tip: Debug failing loop invariants by reasoning inductively, from one iteration to the next

All that remained was to generalize the array index type to range over all positive integers instead of the range 1..5, and to allow unconstrained arrays whose length is not known statically:

Because we’ve used so far relative attributes A’First/A’Last instead of the equivalent magic numbers 0/5, the adjustments needed are minimal.

Tip: Use language features to facilitate the generalization of assertions and ghost code

By reviewing the final code, I realized that the last loop invariant could be written without quantification, as we already get that the array is sorted up to index I-1:

Tip: Simplify ghost code once the program is proved

That concludes with the functional proof of this program.

Or does it? We have not proved here that the result of sorting is a shuffling of the entry. This is doable with SPARK, but just… not easy. In 99.9% of the cases, in practice you’d stop here because:

• It is obvious from looking at the code to see that the result is a shuffling of the entry, as A is only modified by swapping two of its elements. So this can be verified by review easily.

• Doing it by proof brings not much more assurance than the review, but a high cost both for the initial proof and for maintenance of the contracts and lemmas as the code or the tools evolve.

Tip: Don’t prove what you don’t need to prove

To recap, we saw 18 tips that could greatly facilitate your use of proof with SPARK (or any similar program proof environment):

Tip: Start small (simple small data types, a single subprogram)
Tip: Start with a passing test
Tip: Use proof automation (and turn up the knob)
Tip: Avoid the Assertocalypse
Tip: Understand tool messages
Tip: Have an expert on call
Tip: Beware the frame condition
Tip: Use the right tool configuration (and switches!)
Tip: Understand the code that you want to prove
Tip: Define suitable types with the tightest constraints
Tip: Define suitable expression functions for important properties
Tip: Use pen-and-paper to really understand the code that you want to prove
Tip: Execute assertions during tests to help debug them
Tip: Debug failing assertions by running tests with assertions in the debugger
Tip: Debug failing loop invariants by reasoning inductively, from one iteration to the next
Tip: Use language features to facilitate the generalization of assertions and ghost code
Tip: Simplify ghost code once the program is proved
Tip: Don’t prove what you don’t need to prove

Here is the final code for our version of the Stupid Sort algorithm: