With the recent addition of a Manual Proof capability in SPARK 18, it is worth looking at an example which cannot be proved by automatic provers, to see the options that are available for proving it with SPARK. The following code is such an example, where the postcondition of Do_Nothing cannot be proved with provers CVC4 or Z3, although it is exactly the same as its precondition:

The issue is that SMT provers that we use in SPARK like CVC4 and Z3 do not recognize the similarity between the property assumed here (the precondition) and the property to prove (the postcondition). To such a prover, the formula to prove (the Verification Condition or VC) looks like the following in SMTLIB2 format:

We see here some of the encoding from SPARK programming language to SMTLIB2 format: the standard integer type Integer is translated into an abstract type integer, with a suitable projection to_rep from this abstract type to the standard Int type of mathematical integers in SMTLIB2; the array types T1 and T2 are translated into SMTLIB2 Array types. The precondition, which is assumed here, is directly transformed into a universally quantified axiom (starting with "forall"), while the postcondition is negated and joined with the other hypotheses, as an SMT solver will try to deduce an inconsistency to prove the goal by contradiction. So the negated postcondition becomes:

The existentially quantified variable X becomes a constant x in the VC, with assertions stating its bounds 1 and 10, and the universal quantification becomes another axiom.

Now it is useful to understand how SMT solvers deal with universally quantified axioms. Obviously, they cannot "try out" every possible value of parameters. Here, the quantified variable ranges over all mathematical integers! And in general, we may quantify over values of abstract types which cannot be enumerated. Instead, SMT solvers find suitable "candidates" for instantiating the axioms. The main technique to find such candidates is called trigger-based instantiation. The SMT solver identifies terms in the quantified axiom that contain the quantified variables, and match them with the so-called "ground" terms in the VC (terms that do not contain quantified or "bound" variables). Here, such a term containing x in the first axiom is (to_rep (select (select tab x) y)), or simply (select tab x), while in the second axiom such a term containing y could be (to_rep (select (select tab x) y)) or (select (select tab x) y). The issue with the VC above is that these do not match any ground term, hence neither CVC4 nor Z3 can prove the VC.

Note that Alt-Ergo is able to prove the VC, using the exact same trigger-based mechanism, because it considers (select tab x) from the second axiom as a ground term in matching. Alt-Ergo uses this term to instantiate the first axiom, which in turn provides the term (select (select tab x) sko_y) [where sko_y is a fresh variable corresponding to the skolemisation of the existentially quantified variable y]. Alt-Ergo then uses this new term to instantiate the second axiom, resulting in a contradiction. So Alt-Ergo can deduce that the VC is unsatisfiable, hence proves the original (non-negated) postcondition.

I am going to consider in the following alternative means to prove such a property, when all SMT provers provided with SPARK fail.

solution 1 - use an alternative automatic prover

As the property to prove is an exact duplication of a known property in hypothesis, a different kind of provers, called provers by resolution, is a perfect fit. Here, I'm using E prover, but many others are supported by the Why3 platform used in SPARK, and would be as effective. The first step is to install E prover from its website (www.eprover.org) or from its integration in your Linux distro. Then, you need to run the executable why3config to generate a suitable .why3.conf configuration file in your HOME directory, with the necessary information for Why3 to know how to generate VCs for E prover, and how to call it. Currently, GNATprove cannot be called with --prover=eprover, so instead I called directly the underlying Why3 tool and it proves the desired postcondition:

solution 2 - prove interactively

With SPARK 18 comes the possibility to prove a VC interactively inside the editor GPS. Just right-click on the message about the unproved postcondition and select "Start Manual Proof". Various panels are opened in GPS:

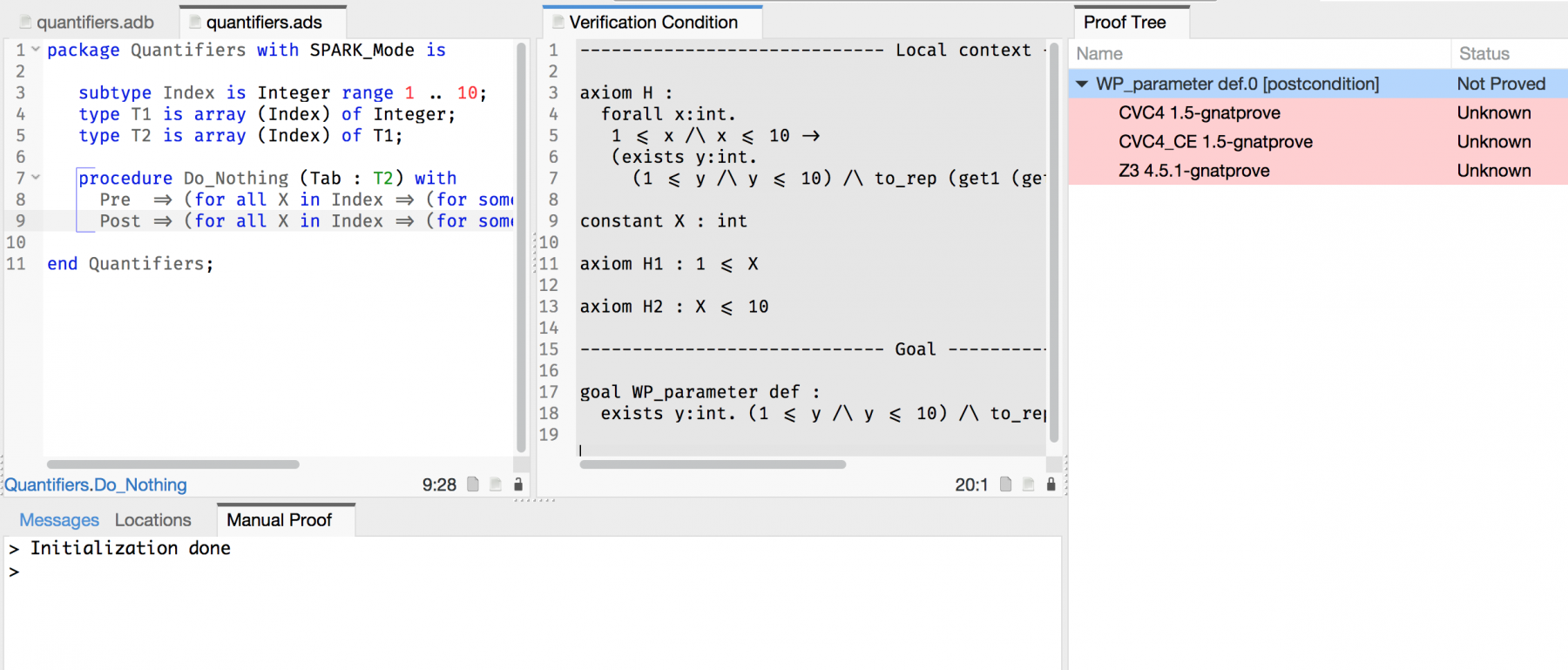
Here, the manual proof is really simple. We start by applying axiom H, as the conclusion of this axiom matches the goal to prove, which makes it necessary to prove the conditions for applying axiom H. Then we use the known bounds on X in axioms H1 and H2 to prove the conditions. And we're done! The following snapshot shows that GPS now confirms that the VC has been proved:

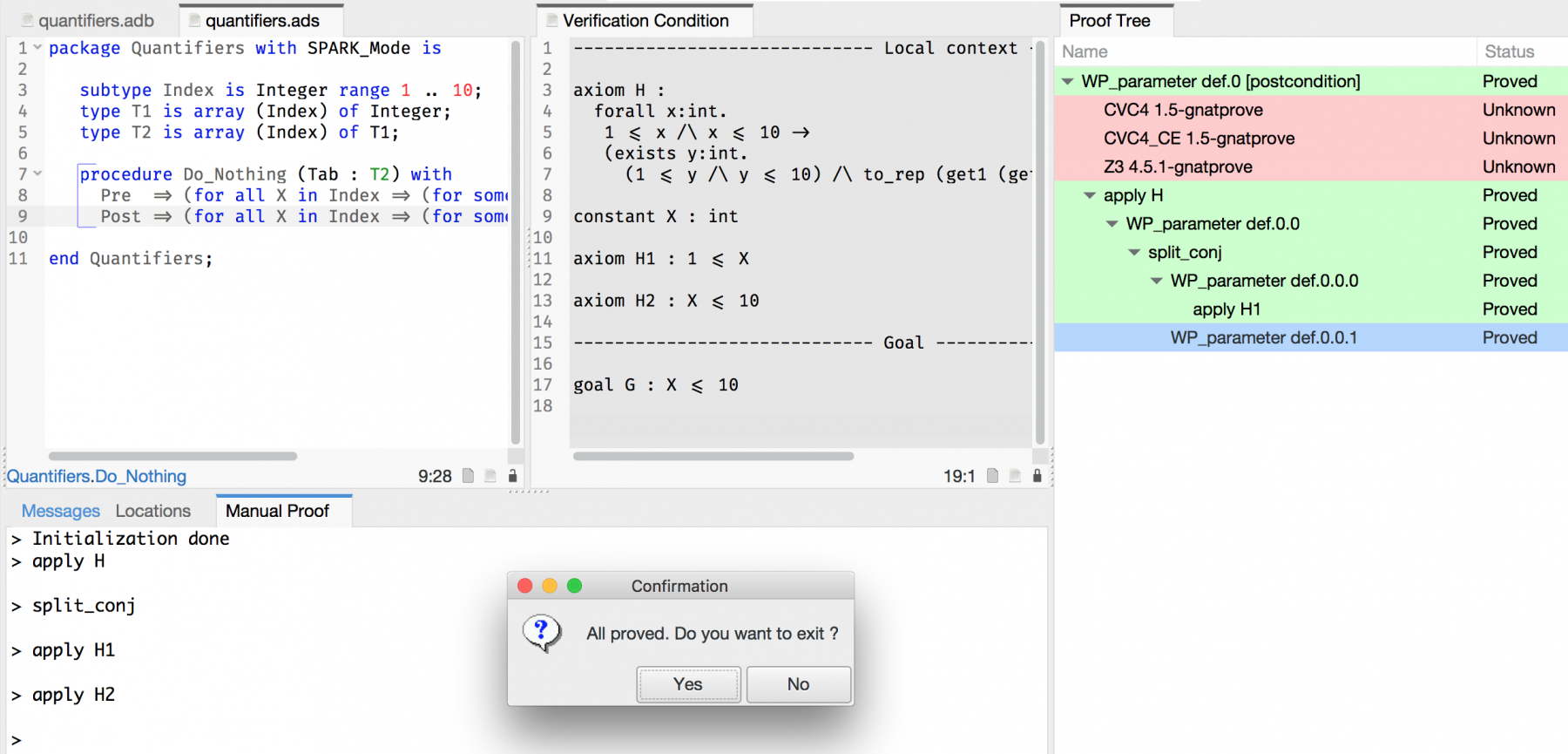
Note that it is possible to call an automatic prover by its name, like "altergo", "cvc4", or "z3" to prove the VC automatically after the initial application of axiom H.

solution 3 - use an alternative interactive prover

It is also possible to use powerful external interactive provers like Coq or Isabelle. You first need to install these on your machine. GNATprove and GPS are directly integrated with Coq, so that you can right-click on the unproved postcondition, select "Prove Check", then manually enter the switch "--prover=coq" to select Coq prover. GPS will then open CoqIDE on the VC as follows:

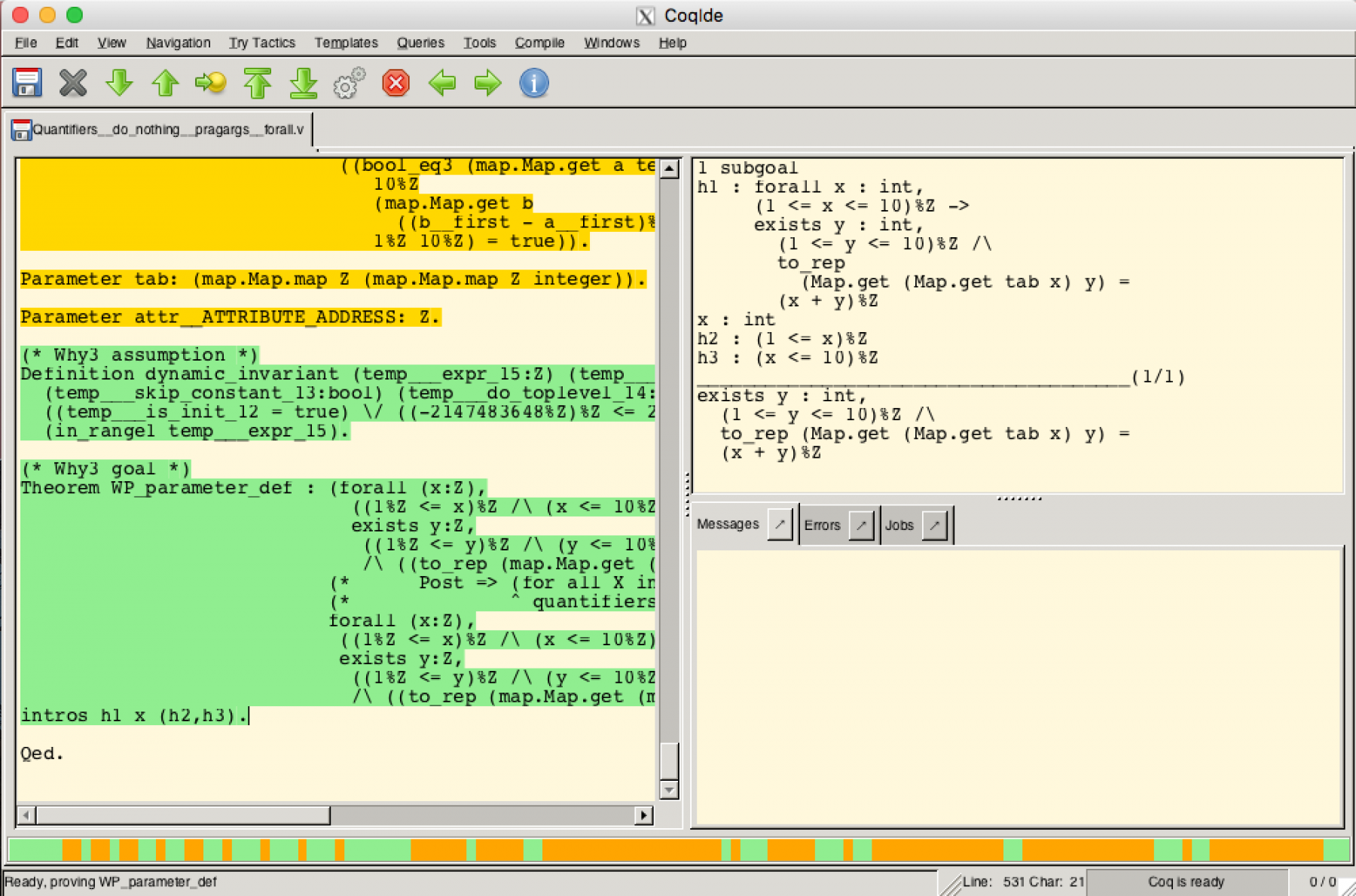
The proof in Coq is as simple as before. Here is the exact set of tactics to apply to reproduce what we did with manual proof in GPS:

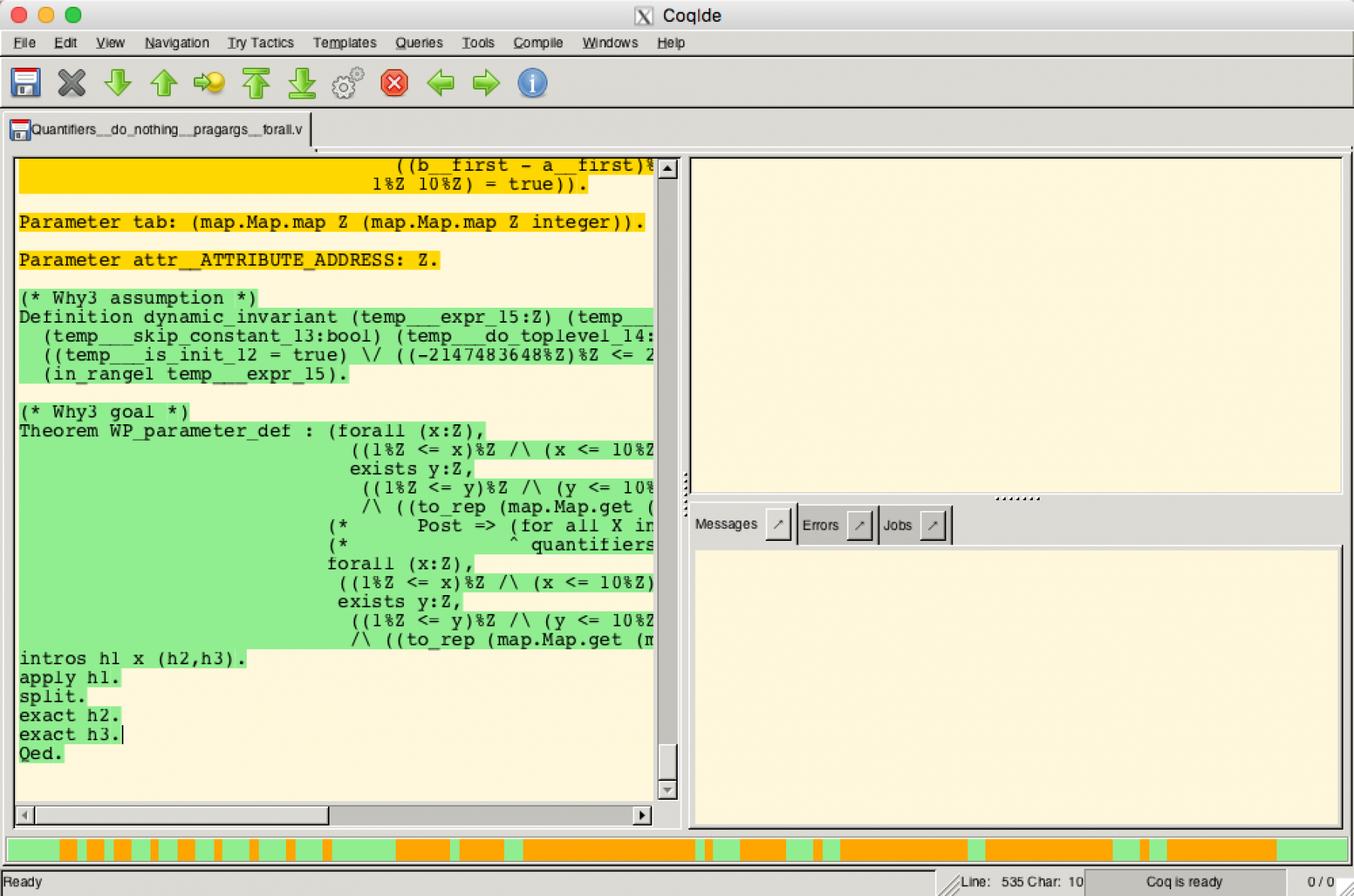
Note that the tactic "auto" in Coq proves this VC automatically.

What to Remember

There are many ways forward that are available when automatic provers available with GNATprove fail to prove a property. We already presented in various occasions the use of ghost code. Here we described three other ways: using an alternative automatic prover, proving interactively, and using an alternative interactive prover.

[cover image of Kurt Gödel, courtesy of WikiPedia, who demonstrated in fact that no all true properties can be ever proved]