Tetris was the first computer game played in space but let's review our ambitions for the time and try to implement it on a Raspberry Pico first.

This idea appeared during my internship at AdaCore. The main purpose of my internship was to explore the possibilities of formal verification in device drivers using SPARK. It seemed both very challenging and valuable to prove such low-level code to ensure safety and security. You can find a report on the process of “SPARKifying” drivers in the previous post. For the internship, I worked more specifically on the Raspberry Pico as there are drivers written in Ada available already. This microcontroller also has a lot of peripherals which offer us the possibility to do a lot of projects on it, so we found it interesting to try to do an entire project on it, fully proved in SPARK.

It's worth noting that some of the SPARK Tetris game code used here was first introduced in one of the first posts on this blog. But unlike this article, our goal is to prove the Tetris and the drivers.

Presentation of the Raspberry Pico

Let's first start with a quick presentation of what Raspberry Pico is.

The Raspberry Pico is composed of a microcontroller RP2040 and multiple GPIO (General Purpose Input Output) which allow us to make a lot of embedded applications with it. If you are not familiar with microcontrollers or Raspberry Pico, I recommend you to watch this short video to have some basic knowledge about the device.

The board is mainly developed to be programmed in MicroPython and C/C++ but there are many projects that use other languages like Rust or Ada. This Ada library was the base of our project.

I then started to convert the different packages of the library to SPARK. Due to the conversion some features had to be removed like the support of the abstraction to HAL (Hardware Abstraction Layer). See the previous post for more details.

After the modification of a few interesting packages like UART and SPI protocol drivers, we found it interesting to create an application using these packages. The purpose was to have a fully proven program which uses the library. Making a Tetris game was a good solution as the game was already almost proved in a previous project and we had a screen for the Raspberry Pi Pico to display the game.

Configuration of the Pico Display

For the TETRIS project, I connected to the Pico an extension board with a screen: the “Pico Display”. To use the Pico Display, I had to write a package to support its functionality. I haven't implemented all the functions that the display allows but only those that were required for the project. I based my work on Ada Drivers Library to be able to draw some shapes (see below) and for the initialization and transmission of the data to the screen with SPI I've looked at this driver and the documentation of the LCD screen.

Bresenham algorithm

To avoid making this blog post too long, in this section we will focus on one proof in particular.

To implement some basic functions of a display, drawing a line is a must-have in a package. But a screen is not something continuous as it is composed by pixels.

In order to determine which pixels are affected when drawing a line we apply the Bresenham algorithm. I will give you a little overview about what it is, but if you want to learn more about the algorithm you can find more details in the wikipedia page here. Like the rest of the code, this algorithm had to be proven with SPARK.

I will walk you through the algorithm construction and its proof.

To simplify and clarify our problems, assume a few initial hypotheses:

• We suppose that DX (the length on the horizontal axis) is bigger than DY (the length on the vertical axis)

• Xmin and Ymin (the coordinates of the start pixel) are respectively smaller than Xmax and Ymax (the coordinates of the last pixel).

The principle of the algorithm is to increment X from the start point to the end point.

We can also add a loop invariant, so that the loop's exit condition is that X has reached its maximum value, thus we have :

X <= Xmax

To draw the line, we have to "choose" Y because sometimes the real line goes through two different pixels. Let's take this simple scheme to represent our problem.

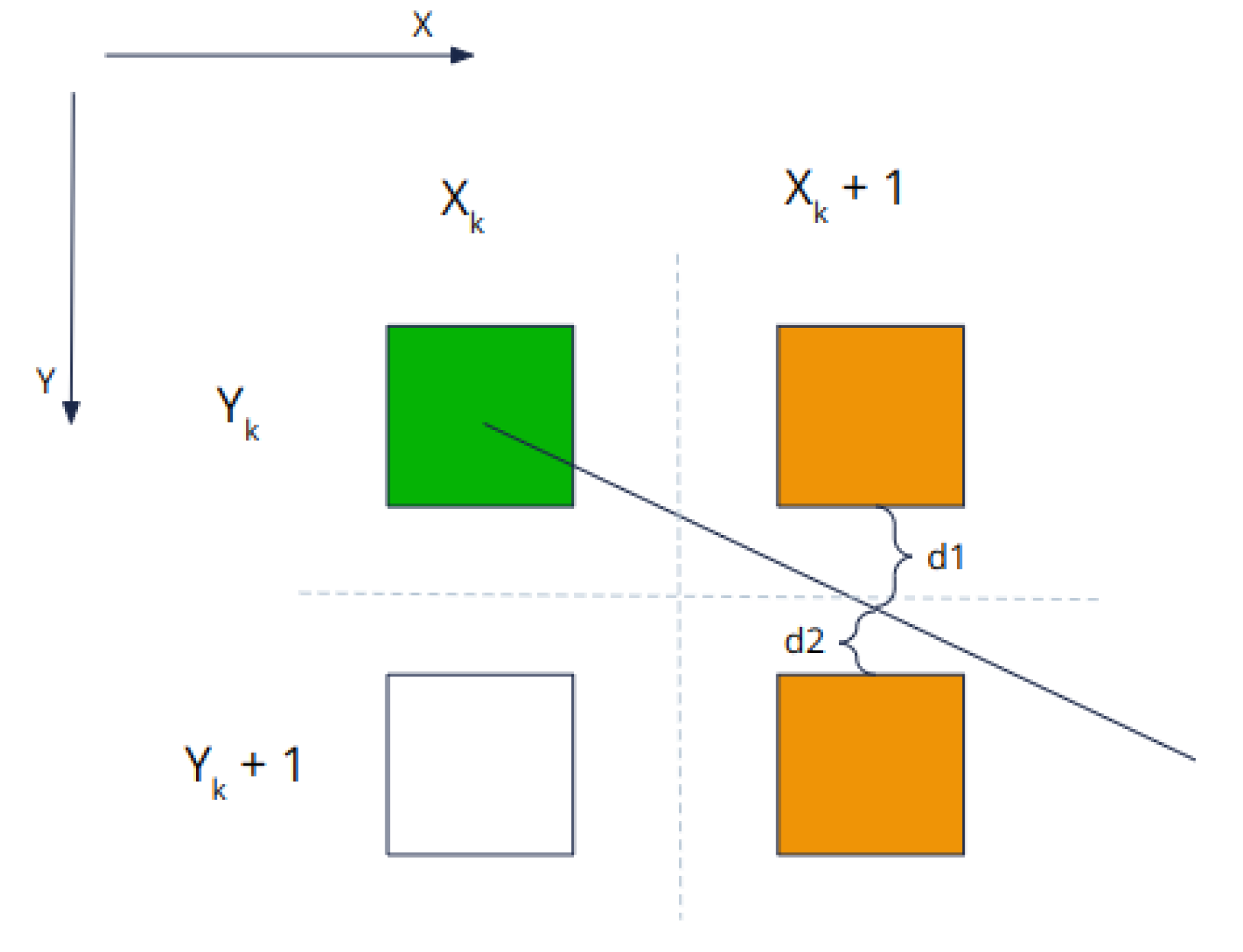
Like I said before, we increase X step by step so the next X coordinate will necessarily be Xk + 1, but as the line passes through two Y pixels the purpose of the algorithm is to determine whether we have to choose Yk or Yk + 1.

To determine it, the first approach is to look at the distance between the desired line and the two pixels and to choose Yk if d1 is smaller than d2 and Yk + 1 otherwise.

We can introduce a new parameter D which is d1 - d2 and we will compare it to 0 to know which pixel to choose.

After a few calculations, we have the value of the decision parameter D and we can add it to the loop invariants.

D= 2 dy (xk - xmin + 1)- dx (2 (yk - ymin)+ 1)

Now we have to construct the algorithm, so we know the computation to do at each iteration of the loop. Let's compute the difference between the current decision parameter D and parameter to the next iteration.

Dnext -Dk = 2 dy (xnext - xk)- 2dx (ynext - yk)

Then we must make a disjunction between two cases for Ynext (Xnext is Xk+1 in both cases) :

• Case 1 : ynext = yk (D <= 0)

Dnext -Dk = 2 dy (xk +1 - xk)- 2dx (yk - yk)

Dnext =Dk + 2 dy

So we have Dnext <= 2 dy

• Case 2 : ynext = yk+1 (D > 0)

Dnext -Dk = 2 dy (xk +1 - xk)- 2dx (yk+1 - yk)

Dnext =Dk + 2 dy - 2dx

So we have Dnext >= 2 (dy - dx)

Let's convert our algorithm to code our algorithm, as we have more information about it now.

The algorithm is now complete but we need to add some loop invariants to specify Y value.

We know that Ymin <= Y, thus Ymax - Y <= DY

Let's compute the value of D when Y = Ymax

D = 2 * DY * (X - Xmax + 1) - DX

We can now majorize the decision parameter D by 0 whatever the value of X is when Y=Ymax. So as D < 0, Y will never be increased when it reaches Ymax thus we can affirm Y <= Ymax.

The last step of the algorithm is to compute the initial value of D taking X=Xmin and Y=Ymin :

D := 2 * DY - DX

So after we add the last invariants needed and the initial value of D we obtain my version of the Bresenham algorithm which is proved :

Running the game

The Tetris game on the Raspberry is proven which shows that such projects are possible in SPARK and extend the range of possibilities. It's important to notice that in the entire project, we were mainly interested in proving the absence of runtime errors. As runtime errors indicate that the device configuration or the functional requirements were not proven. However, certain aspects such as volatile variables or pointers can be blocking and require transformations that were possible in our case but will not always be.

If you have a Raspberry Pico and the display you can try this version of Tetris. You can find a release with the UF2 file to put on your Raspberry on this repository: https://github.com/elsaferrara/tetris and don't hesitate to give me feedback or comments.