This post presents my work as an intern within the SPARK team, which took place from February to August 2025. SPARK refers both to an Ada-derived programming language targeted at functional specification and static verification, and to a set of development and verification tools for that language. The objective of this software is to mathematically guarantee the absence of runtime errors and the conformance of a program with its specifications.

When analysing a SPARK program with GNATprove, some verification conditions might remain unproven, whether because of a defect in the user’s code, contracts that are too weak, or sometimes because of a tool limitation. As a consequence of the way the SPARK toolset works, it can be complicated for the average user to understand why a proof fails in their program. In this context, an effective way of helping developers is to provide them with counterexamples. We call counterexamples (CE), SPARK subprogram input values that would lead to invalid executions (out-of-bounds access, division by zero, integer overflow, exceptions, etc.). Such CEs ​​can be of great help to the user because they allow them to understand why GNATprove cannot prove their code, how contracts must be refined, as well as give them values ​​to test against.

One can also think of these CEs as test values, since we have the option to check SPARK contracts at run-time, we know in advance that the values can dynamically produce an error. GNATprove was already able to provide CEs for some subprograms, but this feature was relatively limited before my internship, especially when it came to dealing with complex branching conditions and data types. The project I worked on during my internship was therefore to take advantage of AdaCore's dynamic analysis suite (GNAT DAS) to improve the counter-example technology. This involved two main approaches:

• Use the value generation techniques (TGEN) from the GNAT DAS toolset to improve the generation of counterexamples. This is done using dynamic code analysis and coverage analysis to obtain valid candidates in a wider variety of cases.
  

• Use GNATtest to generate executable test cases from counterexamples, to provide a powerful debugging tool.

In order to generate CE candidates for a SPARK program, GNATprove delegates the formal verification operations to Why3, a deductive verification software platform. To this end, a sub-tool of GNATprove is GNAT2Why, which is able to translate SPARK code into WhyML, the language handled by Why3. Why3 then performs further transformations on this input and then invokes different provers (Z3, Colibri, Alt-Ego, Coq, etc.). These return a verdict and – in case of a negative result – potential candidate counter-examples, which are then sent back to GNATprove.

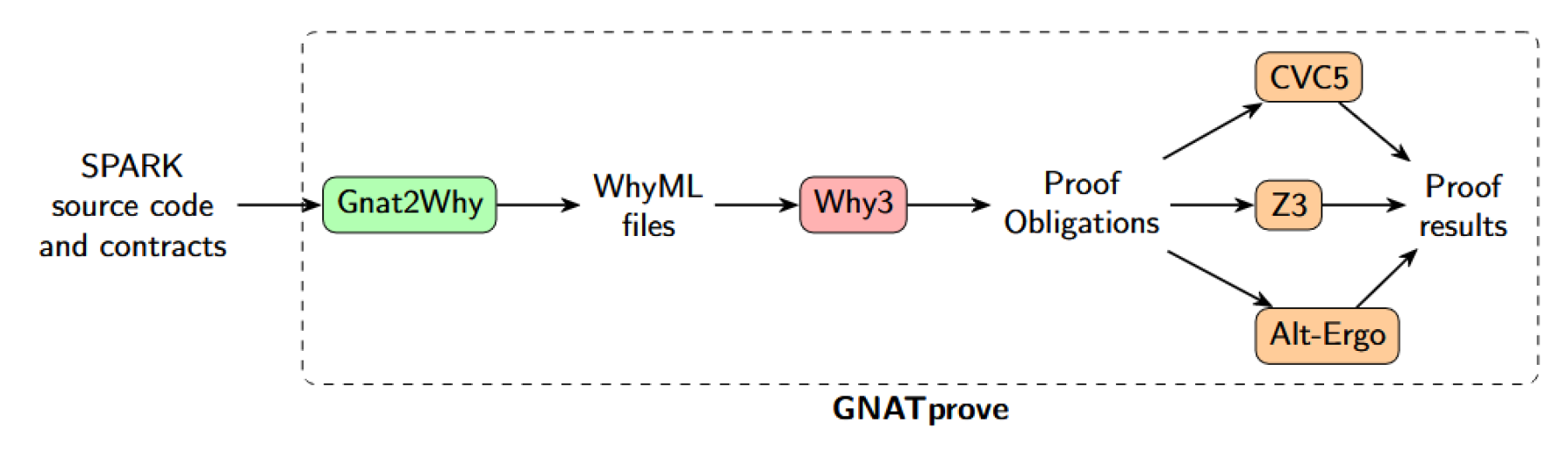
The last step, within GNATprove, is the Runtime Assertion Checker, which statically checks whether the CE candidates supplied by Why3 are effective (i.e., ones that actually cause an error). In situations for which the verdict is negative and Why3 and its provers fail to provide valid CE candidates, GNATprove can invoke other methods of finding some. Among other techniques, it can try to generate random values, test the limits of a type, or test remarkable values.

For example, let's consider the following subprogram written in SPARK:

If we try to verify it with GNATprove we obtain the following verdict:

GNATprove detected that the subprogram could cause an error at runtime and provided the input value (1/128, -1/128) as a counter-example for the user.

Improve Counter Example Fuzzing with Gnattest

However, GNATprove alone is not able to validate and print CE for all failed proof attempts.

Let’s consider a SPARK developer who wants to write a subprogram that computes the sum of an array of integers. One can come up with the following function:

In this code, the developer did not think about the risk of an overflow in S. If they were to use GNATprove to analyze this subprogram, the following message would be displayed:

Here, a ‘medium’ severity verdict means that GNATprove is unable to prove the absence of an overflow runtime error. If GNATprove was sure the check could fail, because it found a counter-example, it would give a verdict with a ‘high’ severity and print the CE. Here, we cannot assert that the proof result is not a false positive. This means that all the counter-example value generation and validation steps have not delivered a proper CE. GNATprove either had no CE candidate from any source or was not able to verify them with the Runtime Assertion Checker. The absence of a counter-example value here can make the error message more complex for the user to interpret, as it does not give them an intuition as to why the proof fails.

The solution I implemented to obtain more counter-examples is to use GNATtest as a test value generator and use these values as CE candidates. It works by generating a large number of parameter sets for the subprogram being analyzed and storing the generated values in an intermediate file. GNATprove can then be invoked from this file and use it as a counter-example candidate bank, sometimes enabling it to find suitable candidates for functions for which all other methods fail. In order to automate the whole process, I wrote a script that performs all steps for a single subprogram, currently available in the spark2014 github repository.

If we use this script on the Sum function above, we obtain:

Here, the verdict is ‘high’, meaning that GNATprove is certain that a runtime error can happen, and provides a value that indeed would cause the error. With this verdict, the developer knows for sure that the negative proof result does come from an error in their code, and not from a tool limitation. GNATprove also provides a value that can be used to reproduce the error locally, which can be of great help to debug erroneous code.

Better Generation With Gnatfuzz

This simple GNATprove/GNATtest integration is however limited in terms of the range of cases for which it is genuinely capable of finding counter-examples. Indeed, if the set of theoretical counter-examples is a very small subset of the possible inputs to the program, GNATtest is unlikely to find even one counter-example, as it does not analyze the program before proposing values. As a way of making the counter-example generation more forehanded, I was able to use the GNATfuzz white-box fuzzer in order to add coverage analysis and symbolic execution to the CE value generation pipeline. Making it able to cover more different branches and find checks that fail for very specific values only.

For example, let’s modify the previous Sum function so that the statement that causes the proof to fail is hard to reach:

Here, GNATtest alone would not be able to find a valid counter-example for the potential overflow within a reasonable period of time. For example, if we try to generate a thousand test cases, no probative values are found for this check:

Using GNATfuzz here allows us to make more educated guesses thanks to the better code analysis. If we run GNATprove on the function above, this time using GNATfuzz as the candidate provider, we do obtain a valid CE:

My work currently outperforms the CE generation of GNATprove for a wide variety of subprograms, specifically those that use floats, arrays, or complex record datatypes, which are notoriously difficult to handle in static analysis.

Executable Tests Generation

When we obtain counterexample values, it is interesting to extract as much information as possible for the user. This was the second main topic of my internship. The approach that has been pointed out to me in this direction is the automatic generation of executable test cases, once again using GNATtest. This consists of creating Ada functions that execute the original subprogram with the counter-example values as input, in order to reproduce the expected error at runtime, for debugging purposes. GNATtest is able to generate test harnesses for a certain subprogram, by generating its own values. I thus performed the reverse integration described above, i.e. insert values generated by GNATprove into the GNATtest pipeline. This works simply by making GNATtest generate a test harness for the current project, then making GNATprove try to find CE values, and then inserting them into the project generated by GNATtest when they exist. Once again, all these steps can be reproduced using a script, testgen.py, available in spark2014.

Let's take a simple example. One could want to generate a test harness for the Div_Skewed subprogram displayed above. Let’s run the script for such a function:

We can then run such test, and we get:

In this way, one can dynamically reproduce the error scenario indicated by GNATprove’s CE, which can be a great help in understanding why the code is incorrect, as well as giving a sample to debug against.

Conclusion

During this internship, I was able to improve counter-example generation and validation by employing more advanced fuzzing and code analysis techniques from GNATtest and GNATfuzz. It is currently done through an intermediate script, and will soon be integrated directly into the product. This is especially useful in the case of subprograms for which Why3 is not able to hand CE candidates over to GNATprove. Future work includes the orchestration of this integration to make it available directly in GNAT Studio, facilitating its usage. Being able to generate counterexample values and use them to create executable tests should make complex SPARK subprograms easier to debug when proofs fail, thus improving the user experience.