Bitcoin blockchain in Ada: Lady Ada meets Satoshi Nakamoto

by Johannes Kanig – Feb 15, 2018

Bitcoin is getting a lot of press recently, but let's be honest, that's mostly because a single bitcoin worth 800 USD in January 2017 was worth almost 20,000 USD in December 2017. However, bitcoin and its underlying blockchain are beautiful technologies that are worth a closer look. Let’s take that look with our Ada hat on!

So what's the blockchain?

“Blockchain” is a general term for a database that’s maintained in a distributed way and is protected against manipulation of the entries; Bitcoin is the first application of the blockchain technology, using it to track transactions of “coins”, which are also called Bitcoins.

Conceptually, the Bitcoin blockchain is just a list of transactions. Bitcoin transactions in full generality are quite complex, but as a first approximation, one can think of a transaction as a triple (sender, recipient, amount), so that an initial mental model of the blockchain could look like this:

Sender	Recipient	Amount
<Bitcoin address>	<Bitcoin address>	0.003 BTC
<Bitcoin address>	<Bitcoin address>	0.032 BTC
...	...	...

Other data, such as how many Bitcoins you have, are derived from this simple transaction log and not explicitly stored in the blockchain.

Modifying or corrupting this transaction log would allow attackers to appear to have more Bitcoins than they really have, or, allow them to spend money then erase the transaction and spend the same money again. This is why it’s important to protect against manipulation of that database.

The list of transactions is not a flat list. Instead, transactions are grouped into blocks. The blockchain is a list of blocks, where each block has a link to the previous block, so that a block represents the full blockchain up to that point in time:

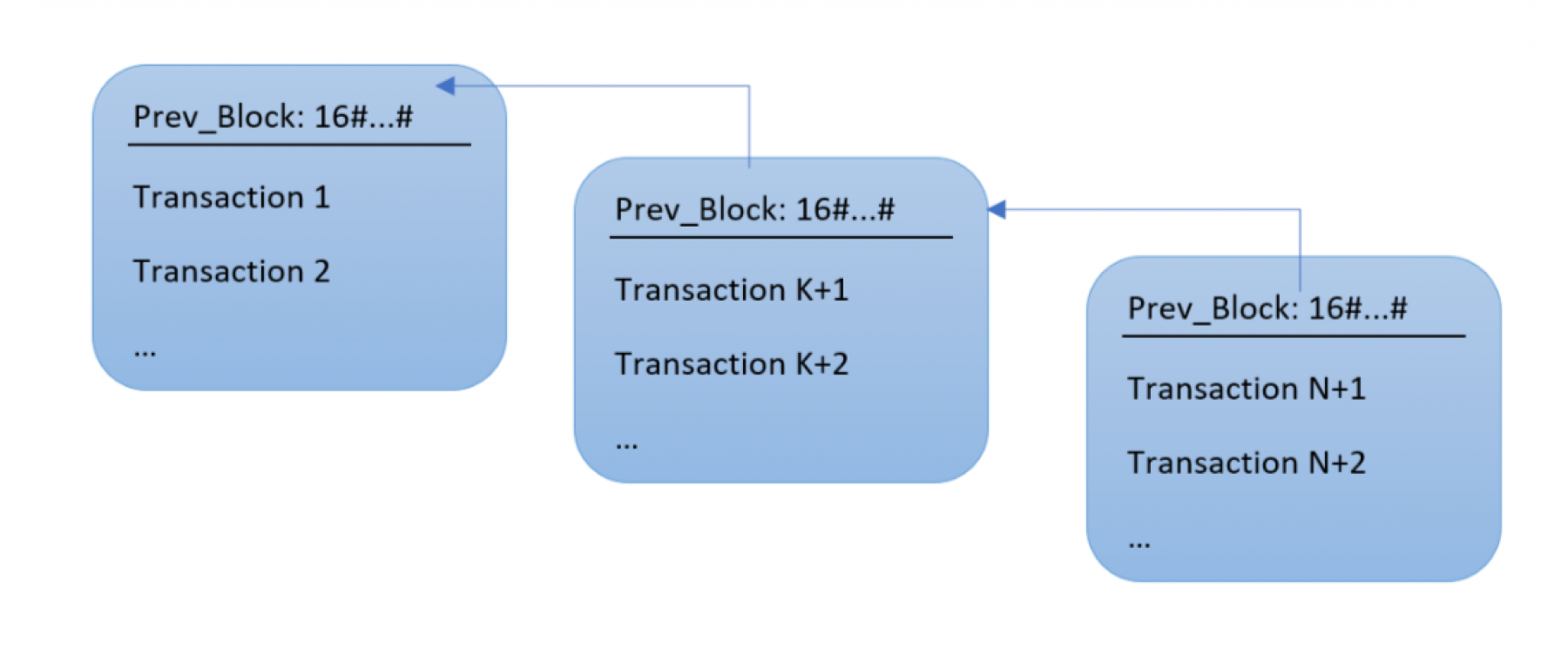
Thinking as a programmer, this could be implemented using a linked list where each block header contains a prev pointer. The blockchain is grown by adding new blocks to the end, with each new block pointing to the former previous block, so it makes more sense to use a prev pointer instead of a next pointer. In a regular linked list, prev pointer points directly to the memory used for the previous block. But the uniqueness of the blockchain is that it's a distributed data structure; it's maintained by a network of computers or nodes. Every bitcoin full node has a full copy of the blockchain, but what happens if members of the network don't agree on the contents of some transaction or block? A simple memory corruption or malicious act could result in a client having incorrect data. This is why the blockchain has various checks built-in that guarantee that corruption or manipulation can be detected.

How does Bitcoin check data integrity?

Bitcoin’s internal checks are based on a cryptographic hash function. This is just a fancy name for a function that takes anything as input and spits out a large number as output, with the following properties:

The output of the function varies greatly and unpredictably even with tiny variations of the input;
It is extremely hard to deduce an input that produces some specific output number, other than by using brute force; that is, by computing the function again and again for a large number of inputs until one finds the input that produces the desired output.

The hash function used in Bitcoin is called SHA256. It produces a 256-bit number as output, usually represented as 64 hexadecimal digits. Collisions (different input data that produces the same output hash value) are theoretically possible, but the output space is so big that collisions on actual data are considered extremely unlikely, in fact practically impossible.

The idea behind the first check of Bitcoin's data integrity is to replace a raw pointer to a memory region with a “safe pointer” that can, by construction, only point to data that hasn’t been tampered with. The trick is to use the hash value of the data in the block as the “pointer” to the data. So instead of a raw pointer, one stores the hash of the previous block as prev pointer:

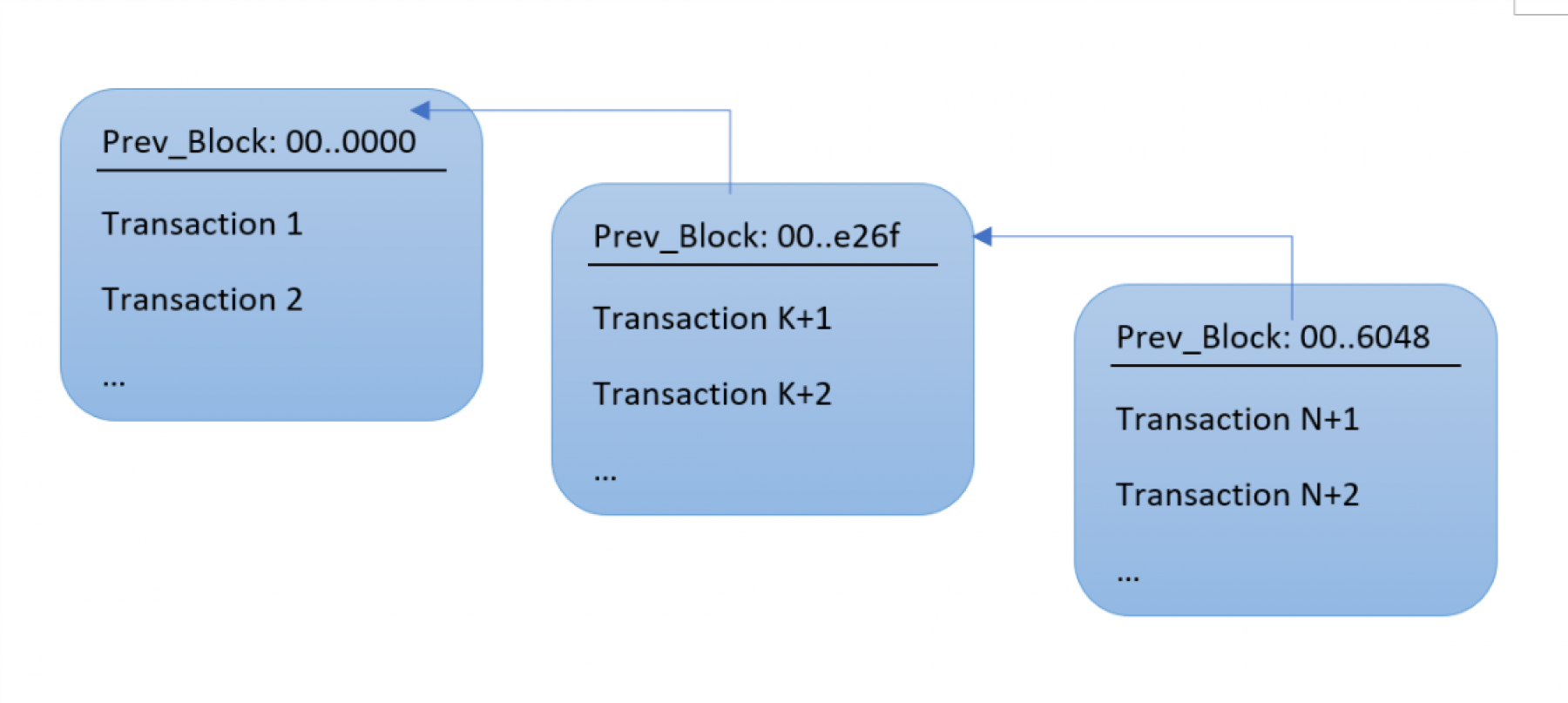
Here, I’ve abbreviated the 256-bit hash values by their first two and last four hex digits – by design, Bitcoin block hashes always start with a certain number of leading zeroes. The first block contains a "null pointer" in the form of an all zero hash.

Given a hash value, it is infeasible to compute the data associated with it, so one can't really "follow" a hash like one can follow a pointer to get to the real data. Therefore, some sort of table is needed to store the data associated with the hash value.

Now what have we gained? The structure can no longer easily be modified. If someone modifies any block, its hash value changes, and all existing pointers to it are invalidated (because they contain the wrong hash value). If, for example, the following block is updated to contain the new prev pointer (i.e., hash), its own hash value changes as well. The end result is that the whole data structure needs to be completely rewritten even for small changes (following prev pointers in reverse order starting from the change). In fact such a rewrite never occurs in Bitcoin, so one ends up with an immutable chain of blocks. However, one needs to check (for example when receiving blocks from another node in the network) that the block pointed to really has the expected hash.

Block data structure in Ada

To make the above explanations more concrete, let's look at some Ada code (you may also want to have bitcoin documentation available).

A bitcoin block is composed of the actual block contents (the list of transactions of the block) and a block header. The entire type definition of the block looks like this (you can find all code in this post plus some supporting code in this github repository):

type Block_Header is record
      Version : Uint_32;
      Prev_Block : Uint_256;
      Merkle_Root : Uint_256;
      Timestamp : Uint_32;
      Bits : Uint_32;
      Nonce : Uint_32;
   end record;

   type Transaction_Array is array (Integer range <>) of Uint_256;

   type Block_Type (Num_Transactions : Integer) is record
      Header : Block_Header;
      Transactions : Transaction_Array (1 .. Num_Transactions);
   end record;

As discussed, a block is simply the list of transactions plus the block header which contains additional information. With respect to the fields for the block header, for this blog post you only need to understand two fields:

Prev_Block a 256-bit hash value for the previous block (this is the prev pointer I mentioned before)
Merkle_Root a 256-bit hash value which summarizes the contents of the block and guarantees that when the contents change, the block header changes as well. I will explain how it is computed later in this post.

The only piece of information that’s missing is that Bitcoin usually uses the SHA256 hash function twice to compute a hash. So instead of just computing SHA256(data), usually SHA256(SHA256(data)) is computed. One can write such a double hash function in Ada as follows, using the GNAT.SHA256 library and String as a type for a data buffer (we assume a little-endian architecture throughout the document, but you can use the GNAT compiler’s Scalar_Storage_Order feature to make this code portable):

with GNAT.SHA256; use GNAT.SHA256;

   function Double_Hash (S : String) return Uint_256 is
      D : Binary_Message_Digest := Digest (S);
      T : String (1 .. 32);
      for T'Address use D'Address;
      D2 : constant Binary_Message_Digest := Digest (T);

      function To_Uint_256 is new Ada.Unchecked_Conversion
        (Source => Binary_Message_Digest,
         Target => Uint_256);
   begin
      return To_Uint_256 (D2);
   end Double_Hash;

The hash of a block is simply the hash of its block header. This can be expressed in Ada as follows (assuming that the size in bits of the block header, Block_Header’Size in Ada, is a multiple of 8):

function Block_Hash (B : Block_Type) return Uint_256 is
      S : String (1 .. Block_Header'Size / 8);
      for S'Address use B.Header'Address;
   begin
      return Double_Hash (S);
   end Block_Hash;

Now we have everything we need to check the integrity of the outermost layer of the blockchain. We simply iterate over all blocks and check that the previous block indeed has the hash used to point to it:

declare
   Cur : String :=
     "00000000000000000044e859a307b60d66ae586528fcc6d4df8a7c3eff132456";
   S : String (1 ..64);
begin
   loop
      declare
         B : constant Block_Type := Get_Block (Cur);
      begin
         S := Uint_256_Hex (Block_Hash (B));
         Put_Line ("checking block hash = " & S);
         if not (Same_Hash (S,Cur)) then 
            Ada.Text_IO.Put_Line ("found block hash mismatch");
         end if;
         Cur := Uint_256_Hex (B.Prev_Block);
      end;
   end loop;
end;

A few explanations: the Cur string contains the hash of the current block as a hexadecimal string. At each iteration, we fetch the block with this hash (details in the next paragraph) and compute the actual hash of the block using the Block_Hash function. If everything matches, we set Cur to the contents of the Prev_Block field. Uint_256_Hex is the function to convert a hash value in memory to its hexadecimal representation for display.

One last step is to get the actual blockchain data. The size of the blockchain is now 150GB and counting, so this is actually not so straightforward! For this blog post, I added 12 blocks in JSON format to the github repository, making it self-contained. The Get_Block function reads a file with the same name as the block hash to obtain the data, starting at a hardcoded block with the hash mentioned in the code. If you want to verify the whole blockchain using the above code, you have to either query the data using some website such as blockchain.info, or download the blockchain on your computer, for example using the Bitcoin Core client, and update Get_Block accordingly.

How to compute the Merkle Root Hash

So far, we were able to verify the proper chaining of the blockchain, but what about the contents of the block? The objective is now to come up with the Merkle root hash mentioned earlier, which is supposed to "summarize" the block contents: that is, it should change for any slight change of the input.

First, each transaction is again identified by its hash, similar to how blocks are identified. So now we need to compute a single hash value from the list of hashes for the transactions of the block. Bitcoin uses a hash function which combines two hashes into a single hash:

function SHA256Pair (U1, U2 : Uint_256) return Uint_256 is
      type A is array (1 .. 2) of Uint_256;
      X : A := (U1, U2);
      S : String (1 .. X'Size / 8);
      for S'Address use X'Address;
   begin
      return Double_Hash (S);
   end SHA256Pair;

Basically, the two numbers are put side-by-side in memory and the result is hashed using the double hash function.

Now we could just iterate over the list of transaction hashes, using this combining function to come up with a single value. But it turns out Bitcoin does it a bit differently; hashes are combined using a scheme that's called a Merkle tree:

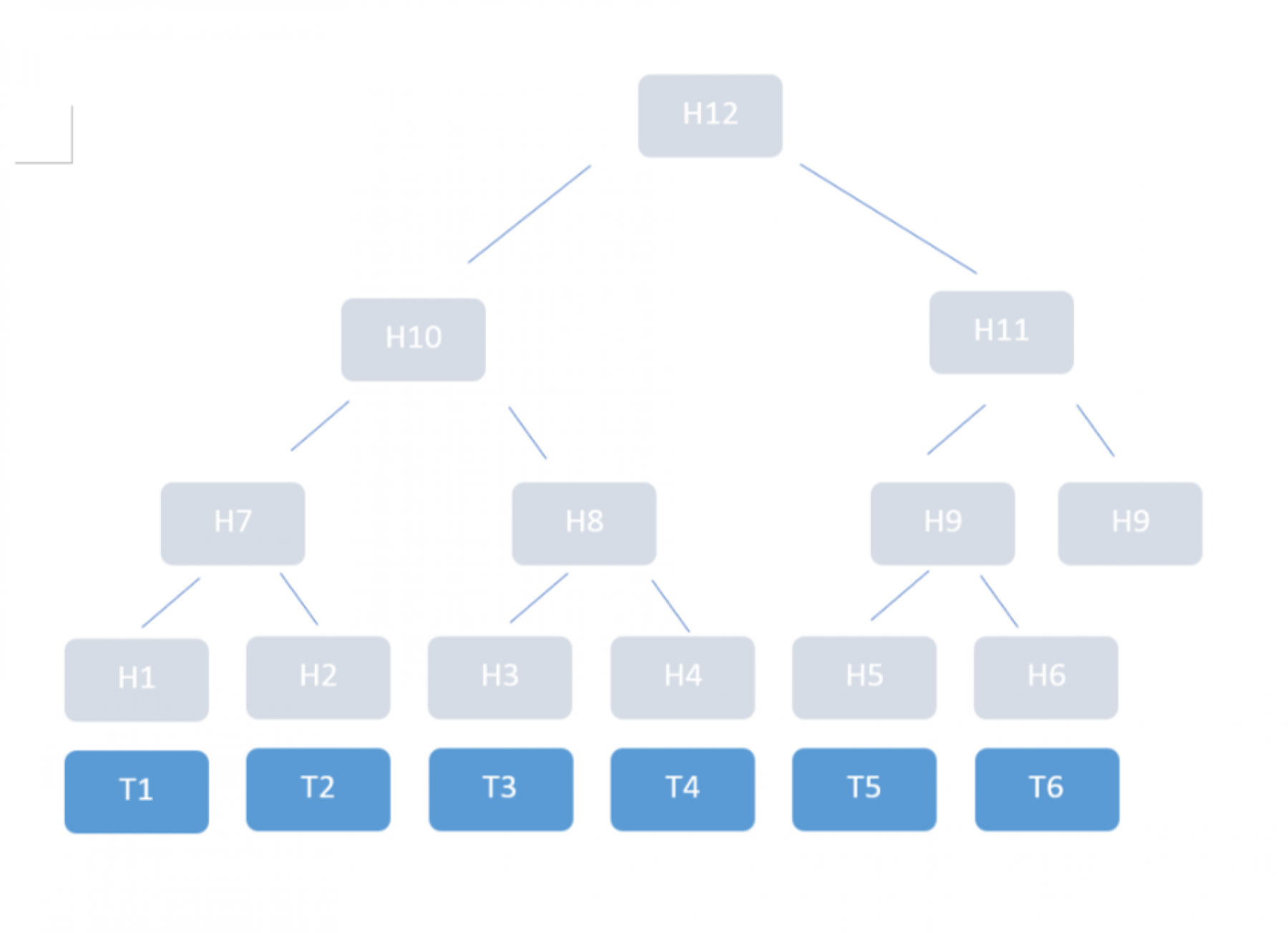
One can imagine the transactions (T1 to T6 in the example) be stored at the leaves of a binary tree, where each inner node carries a hash which is the combination of the two child hashes. For example, H7 is computed from H1 and H2. The root node carries the "Merkle root hash", which in this way summarizes all transactions. However, this image of a tree is just that - an image to show the order of hash computations that need to be done to compute the Merkle root hash. There is no actual tree stored in memory.

There is one peculiarity in the way Bitcoin computes the Merkle hash: when a row has an odd number of elements, the last element is combined with itself to compute the parent hash. You can see this in the picture, where H9 is used twice to compute H11.

The Ada code for this is quite straightforward:

function Merkle_Computation (Tx : Transaction_Array) return Uint_256 is
      Max : Integer :=
          (if Tx'Length rem 2 = 0 then Tx'Length else Tx'Length + 1);
      Copy : Transaction_Array (1 .. Max);
   begin
      if Tx'Length = 1 then
         return Tx (Tx'First);
      end if;
      if Tx'Length = 0 then
         raise Program_Error;
      end if;
      Copy (1 .. Tx'Length) := Tx;
      if (Max /= Tx'Length) then
         Copy (Max) := Tx (Tx'Last);
      end if;
      loop
         for I in 1 .. Max / 2 loop
            Copy (I) := SHA256Pair (Copy (2 * I - 1), Copy (2 *I ));
         end loop;
         if Max = 2 then
            return Copy (1);
         end if;
         Max := Max / 2;
         if Max rem 2 /= 0 then
            Copy (Max + 1) := Copy (Max);
            Max := Max + 1;
         end if;
      end loop;
   end Merkle_Computation;

Note that despite the name, the input array only contains transaction hashes and not actual transactions. A copy of the input array is created at the beginning; after each iteration of the loop in the code, it contains one level of the Merkle tree. Both before and inside the loop, if statements check for the edge case of combining an odd number of hashes at a given level.

We can now update our checking code to also check for the correctness of the Merkle root hash for each checked block. You can check out the whole code from this repository; the branch “blogpost_1” will stay there to point to the code as shown here.

Why does Bitcoin compute the hash of the transactions in this way? Because it allows for a more efficient way to prove to someone that a certain transaction is in the blockchain.

Suppose you want to show someone that you sent her the required amount of Bitcoin to buy some product. The person could, of course, download the entire block you indicate and check for themselves, but that’s inefficient. Instead, you could present them with the chain of hashes that leads to the root hash of the block.

If the transaction hashes were combined linearly, you would still have to show them the entire list of transactions that come after yours in the block. But with the Merkle hash, you can present them with a “Merkle proof”: that is, just the hashes required to compute the path from your transaction to the Merkle root. In your example, if your transaction is T3, it's enough to also provide H4, H7 and H11: the other person can compute the Merkle root hash from that and compare it with the “official” Merkle root hash of that block.

When I first saw this explanation, I was puzzled why an attacker couldn’t modify transaction T3 to T3b and then “invent” the hashes H4b, H7b and H11b so that the Merkle root hash H12 is unchanged. But the cryptographic nature of the hash function prevents this: today, there is no known attack against the hash function SHA256 used in Bitcoin that would allow inventing such input values (but for the weaker hash function SHA1 such collisions have been found).

Wrap-Up

In this blog post I have shown Ada code that can be used to verify the data integrity of blocks from the Bitcoin blockchain. I was able to check the block and Merkle root hashes for all the blocks in the blockchain in a few hours on my computer, though most of the time was spent in Input/Output to read the data in.

There are many more rules that make a block valid, most of them related to transactions. I hope to cover some of them in later blog posts.

Posted in #Bitcoin #Blockchain #Ada

About Johannes Kanig

Johannes Kanig is a senior software engineer at AdaCore and developer of the SPARK technology. He received his PhD in formal verification from the University Paris-Sud, France.